Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 14.Problemas - Ex. 75
O peso da coroa de um rei é . Quando suspensa por uma corda leve e totalmente imersa na água, a tensão na corda (o peso aparentemente da coroa é) é igual a . a) Mostre que a densidade relativa da coroa é dada por . Discuta o significado dos limites quando e . b) Se a coroa for de ouro sólido e pesar 12,9 N no ar, qual será o eu peso aparente quando estiver totalmente imersa na água? c) Repita a parte (b) se a coroa for de chumbo sólido com uma camada muito fina de ouro, porém com peso ainda igual a 12,9 N no ar.
Passo 1
Aplicaremos a segunda lei de Newton à coroa. A força de flutuação é dada pelo princípio de Arquimedes.
A variável alvo é a razão , onde ().
Vamos esboçar um diagrama de corpo livre para a coroa.
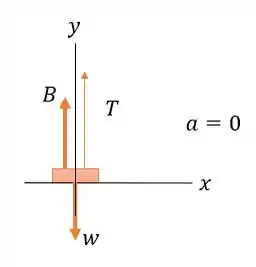
Passo 2
- Assim, aplicando
- "Peso aparente" é igual a na corda quando a coroa é imersa em água. , então é necessário calcular.
- Agora a densidade da coroa é muito próxima da densidade do chumbo;
Temos que
Onde e .
Então,
Usando , onde
Então,
Isso implica que
como era para ser mostrado.
fornece e . Esses valores são consistentes. Se a densidade da coroa for igual à densidade de água, a coroa flutua, totalmente submersa, e a tensão deve ser zero.
Quando , e . Se , então B é desprezível em relação ao peso w da coroa e T deve ser igual a w.
Passo 3
Sabemos que e
Logo
Nos da que
E
Então
Passo 4
Sabemos que agora
Logo
Nos da que
E
Então
Na parte (c) a densidade média da coroa é menor que na parte (b), portanto o volume é maior. B é maior e T é menor. Essas medidas podem ser usadas para determinar se a coroa é ouro maciço, sem danificar a coroa.
Resposta
- Foi mostrado que