Neste problema, você deve deduzir a expressão para a potência média desenvolvida por uma força de excitação sobre um oscilador forçado.
- Mostre que a potência instantânea desenvolvida pela força de excitação é dada por .
- Use a identidade para mostrar que a equação da parte (a) pode ser escrita como .
- Mostre que o valor médio do segundo termo do resultado da parte (b), sobre um ou mais períodos, é zero, e que, portanto, .
- Considerando a equação 14-56 para , construa um triangulo retângulo no qual o lado oposto ao ângulo é e o lado adjacente é , e use este triângulo para mostrar que:
- Use o resultado da parte (d) para eliminar do resultado da parte (c), de forma a poder escrever a potência média desenvolvida como:
Passo 1
Então, galera, essa parece muito difícil a princípio, mas é só a gente ir seguindo as dicas que vai dar bom! Bora lá então!
- A potência média é dada por:
- Agora é só usar aquela relação para .
- A segunda parcela da expressão é . Vamos mostrar que o valor médio de é zero.
- Olha aí o triangulo que ele mandou construir:
- Nós encontramos aí em cima:
Mas a força é função do tempo, de forma que:
E a posição é escrita em função do tempo como:
Derivando essa relação,
Assim, multiplicando pra achar a potencia:
Passo 2
Passo 3
Portanto, a potencia média só depende do primeiro termo. Ele é dado por . Então vamos descobrir o valor médio de
Então a potencia média vai ser dada por:
Passo 4
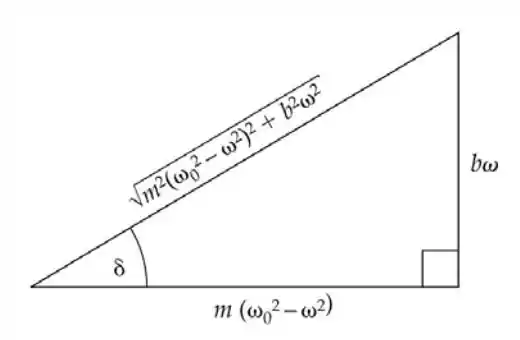
Nele,
Pela equação 14-55 da teoria a gente consegue reduzir essa expressão:
E então:
Passo 5
Substituindo na expressão da potência média:
Mas do item d:
E então:
Resposta
Ei, a resposta está no passo a passo :)