Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 12.1 - Ex. 33
Uma escada, de massa desprezível e comprimento , está apoiada contra uma parede lisa, formando um ângulo com o piso horizontal. O coeficiente de atrito entre a escada e o piso é . Um homem sobe a escada. Até que altura ele pode chegar antes de a escada escorregar?
Passo 1
Oi, gente! Ele quer saber até que altura uma pessoa pode subir numa escada que está inclinada e apoiada na parede. Vamos começar fazendo o diagrama de corpo livre dessa situação, usando os dados que ele deu.
Pra começo de conversa, pensa aqui comigo. Se uma escada tem massa desprezível e está em repouso, parada sob uma superfície, o diagrama de forças da escada sem ninguém em cima é:
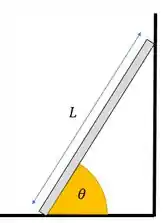
Opa, sem forças? Bem, se não tem peso (já que o enunciado disse que a massa da escada é desprezível), não tem como ter normal, logo nenhuma força vertical. Se está em repouso, não há nenhuma força na horizontal também. Então aí a gente só representou o comprimento da escada e o ângulo que ela faz com a horizontal .
Agora, se um homem sobe na escada, o sistema (homem+escada) ganha massa. Considerando:
- Massa do homem
- Aceleração da Gravidade
- Peso do homem
- Altura em que o homem está em relação ao solo
Teremos:
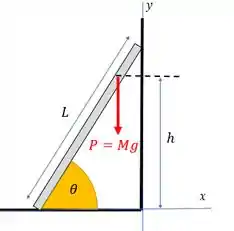
Só que, se tem peso e a escada não está afundando no chão ou na parede, tem que ter força normal! A reação da parede é horizontal, da direita pra esquerda, e a do chão é vertical, de baixo pra cima.
Por fim, como o sistema está em repouso, não queremos que a escada escorregue. Se ela escorregar, a ponta que tá no chão vai se mover da direita pra esquerda. Quem impede esse movimento? Exatamente a força de atrito! O diagrama de forças final será:
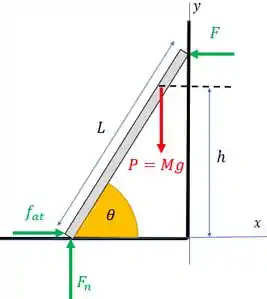
Perceba que não há força de atrito na parede porque o enunciado diz que a parede é lisa, então ela não oferece atrito.
A ideia aqui é perceber que a escada está paradinha, então podemos usar as equações de equilíbrio nas forças que representamos no diagrama
E vamos usa-las para achar o valor de em função dos dados que ele deu. Vamos!
Passo 2
Vamos começar pelo equilíbrio de forças na horizontal e na vertical.
Considerando que forças positivas estão viradas para cima, o somatório de forças na vertical fica
Agora olhando para as forças horizontais, considerando as forças positivas para a direita, temos que
Quem é ? Cara, como a gente quer a altura limite para a escada começar a escorregar, a gente está na situação de iminência do deslizamento. Nessa situação a força de atrito é máxima e vai valer
Como já temos :
E pelo somatório de forças em :
Já temos expressões para todas as nossas forças. Vamos partir para achar .
Passo 3
Para isso vamos usar mais uma equação de equilíbrio: a de torques! Afinal, a escada não está girando. Portanto o somatório de torques será nulo.
Vamos calcular o somatório de torques em relação ao ponto onde a escada encosta no piso, que chamaremos de ponto . E a gente vai considerar que se a força tende a girar a escada no sentido anti-horário, o torque gerado por ela é positivo, caso contrário, negativo.
O torque vai ser dado pelo produto entre a força e , onde é uma distância entre a linha de ação da força e o ponto onde queremos o torque. Sendo que e a força precisam ser perpendiculares.
Para começar, note o seguinte: para as forças e é nulo por que elas estão sendo aplicadas no eixo de rotação! Por esse motivo, elas não contribuem para o torque!
Vamos marcar o de cada força restante no nosso diagrama de corpo livre
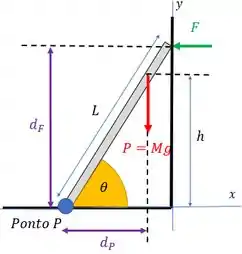
Percebe que é a distância perpendicular entre a linha de aplicação de e o eixo de rotação que passa pelo ponto . E essa força tende a girar a escada no sentido horário, então o torque fica negativo e é
Para achar usamos o triângulo que pode ser encontrado na figura
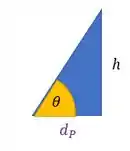
Temos um triângulo retângulo, então podemos escrever
Aí o torque fica
Agora para a força , a distância entre sua linha de ação e é e ela tende a girar nossa escada no sentido anti-horário, então temos
E para achar , usamos o triângulo
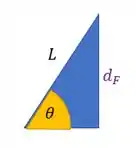
Usando trigonometria
O torque fica
Passo 4
Show, agora vamos montar a equação de equilíbrio
Queremos né? Vamos isolar esse cara:
Lembra que a gente tinha achado as expressões de e de ?
Vamos substituir essas belezinhas
E pronto! Tá na mão! Para que haja equilíbrio (somatório de torques e de forças nula), o valor máximo de deve ser: