Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 11.3 - Ex. 5
Uma escada transportada em um caminhão de bombeiro possui de comprimento. A escada pesa , e o centro de gravidade está situado no seu centro. A escada é articulada em uma extremidade (A) com um eixo de apoio (Figura 11.22); o torque devido ao atrito no eixo pode ser desprezado. A escada é levantada para sua posição mediante uma força aplicada em C por um pistão hidráulico. O ponto C está a do ponto A, e a força exercida pelo pistão faz um ângulo de com a escada. Qual deve ser o módulo de para que a escada esteja na iminência de ser levantada do seu apoio no ponto B? Comece com um diagrama do corpo livre para a escada.
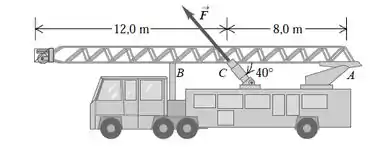
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente encontrar o módulo da força para que a escada esteja na iminência de ser levantada do seu apoio no ponto . Nós sabemos que essa escada tem de comprimento, pesa e o centro de gravidade dela está no seu centro.
Além disso, a escada é levantada para sua posição mediante uma força aplicada em por um pistão hidráulico. O ponto está a do ponto articulado , e a força exercida pelo pistão faz um ângulo de com a escada.
Então, vamos esboçar o diagrama de corpo livre (DCL) do nosso sistema, usar as equações de equilíbrio, fazendo os somatório dos torque (com sentido anti-horário positivo) e das forças, e analisar os nossos resultados.
Vamos lá!
Passo 2
Vamos começar desenhando as forças sobre a escada no DCL:
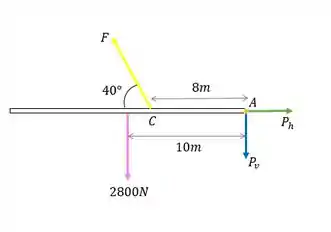
O torque devido a deve equilibrar o torque devido ao peso da escada. Logo, vamos aplicar:
Já que a escada está na iminência de ser levantada, então ainda está em repouso. Logo, o torque resultante deve ser nulo.
Agora vamos aos cálculos para achar .
Passo 3
Pelo esquema desenhado, temos que:
Isso porque apenas a componente vai exercer um torque em relação ao eixo . Subsituindo valores dados,
Como o torque resultante deve ser nulo ():
Então, fazendo as continhas, chegamos a:
A força necessária é maior que o peso da escada, porque o braço do momento para é menor
do que o momento braço para .
Valeu, galera! Até a próxima! 😉