Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 11.3 - Ex. 8
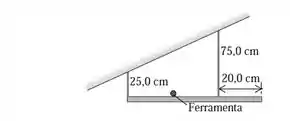
Uma prateleira uniforme de cm e é horizontalmente sustentada por dois cabos verticais presos ao teto inclinado (Figura 11.23). Uma ferramenta muito pequena de é
colocada sobre a prateleira no meio do caminho entre os pontos em que os cabos estão presos. Ache a tensão em cada cabo. Comece com um diagrama do corpo livre para a prateleira.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente encontrar a tensão em cada cabo que sustenta a prateleira. Nós sabemos que essa prateleira tem de comprimento e pesa e que uma ferramenta muito pequena de foi colocada sobre ela, no meio do caminhos entre os cabos.
Sendo assim, vamos começar fazendo o diagrama de corpo livre (DCL) do sistema para entender o que tá acontecendo e quais forças estão agindo. Então, nós vamos aplicar as equações das condições de equilíbrio na prateleira, fazendo o somatório de forças e de torque, para encontrar o valor da tensão em cada cabo.
Vamos lá!
Passo 2
Vamos esboçar o diagrama de corpo livre da situação:
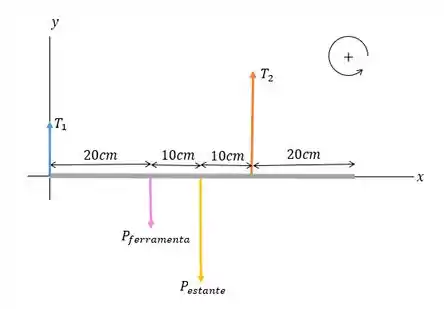
Assim, vamos tomar o eixo na extremidade esquerda da prateleira e convencionar o torque no sentido anti-horário como positivo.
O centro de gravidade da prateleira uniforme está no centro. Então, aplicando a condição de equilíbrio dos torques, temos que:
Assim, isolando a tensão , ficamos com:
Passo 3
E então, aplicando condição de equilíbrio para as forças na vertical, temos que:
Assim, isolando a tensão , temos:
E substituindo os valores dados, encontramos a outra tensão:
Valeu, galera! Até a próxima! 😉