Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 16.1 - Ex. 5
Uma onda senoidal se propaga em uma corda. O tempo necessário para que um ponto da corda se desloque do deslocamento máximo até zero é . Qual é (a) o período e (b) a frequência da onda? (c) O comprimento de onda é ; qual é a velocidade da onda?
Passo 1
Show de bolinhas galerinha, nesse exercicio aqui, o exercício nos deu que uma onda senoidal se propaga em uma corda e o tempo necessário pra que um ponto da corda se desloque do deslocamento máximo até zero é . Sabendo disso, na letra (a), ele quer que a gente encontre o período.
Iradoso, a questão deu só uma informação pra começarmos: o tempo que um ponto da corda leva pra se deslocar do máximo ao zero.
Vamos desenhar a onda senoidal pra descobrir qual grandeza é essa:
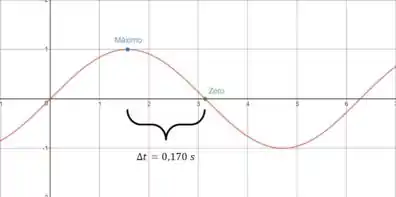
Como não sabemos nada sobre a onda ainda, essa é uma onda de seno qualquer, então desconsidere a escala dos eixos.
Bom, o período é o tempo que o movimento demora pra se repetir. Uma forma de achar ele no gráfico é contar uma subida e uma descida.
Olhando a imagem, dá pra ver que esse intervalo de tempo corresponde a um quarto de um período (metade da metade):
Ou seja, a resposta da letra (a) vai ser:
Belezoca, bora ver como ficam as outras.
Passo 2
(b) Agora queremos a frequência da onda.
Sem problemas, é só fazer o inverso do período:
Passo 3
(c) Agora temos uma informação nova, o comprimento da onda:
E queremos descobrir a velocidade.
Tranquilo, vamos usar essa fórmula aqui:
Pronto!
Resposta
(a) .
(b) .
(c) .