Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 16.1 - Ex. 67

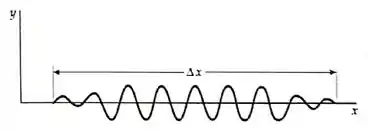
Um diapasão, com frequência natural f 0 , começa a vibrar no tempo t = 0   e é parado após um intervalo de tempo ∆ t . A forma de onda do som, em algum tempo posterior, é mostrada (Figura 16-35) como função de x . Seja N uma estimativa do número de ciclos desta forma de onda. (a) Se ∆ x é o comprimento espacial deste pacote de ondas, qual é a faixa de números de onda ∆ k do pacote? (b) Estime o comprimento de onda médio λ em termos de N e de ∆ x . (c) Estime o número de onda médio k em termos de N e de ∆ x . (d) Se ∆ t é o tempo que leva para o pacote de ondas passar por um ponto no espaço, qual é a faixa de frequências angulares ∆ ω do pacote? (e) Expresse f 0 em termos de N e de ∆ t . (f) O númeor N é incerto em cerca de ±   1   c i c l o . Use a Figura 16-35 para explicar por quê. (g) Mostre que a incerteza no comprimento de onda, devida à incerteza em N , é de 2 π / ∆ x .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Item (a):

Relacionando a duração do pulso com o número de ciclos no intervalo e período de cada ciclo:

∆ t ≈ N T

∆ t = N f 0

Passo 2

Item (b):

Para o comprimento de onda temos:

λ ≈ ∆ x N

Passo 3

Item (c):

Podemos usar a definição para expressar o número de onda:

k = 2 π λ

Do passo 3, temos λ ≈ ∆ x N , portanto:

k = 2 π N ∆ x

Passo 4

Item (d):

Para determinar o interfalo de frequências, usamos ∆ ω ∆ t ∼ 1 logo:

∆ ω ∼ 1 ∆ t

Passo 5

Item (e):

Do Passo 1, temos:

f 0 = N ∆ t

Passo 6

Item (f):

N é incerto porque a forma de onda desaparece gradualmente em vez de parar abruptamente em algum momento. Portanto, onde o pulso começa e para não está bem definido.

Passo 7

Item (g):

Do Passo 3, temos k = 2 π N ∆ x , portanto:

∆ k = 2 π ∆ N ∆ x

Como ∆ N = ± 1 , temos:

∆ k = 2 π ∆ x

Resposta

a ) ∆ t = N f 0

b ) λ ≈ ∆ x N

c ) k = 2 π N ∆ x

d ) ∆ ω ∼ 1 ∆ t

e ) f 0 = N ∆ t

g ) ∆ k = 2 π ∆ x

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em princípio, uma onda com praticamente qualquer forma arbitrária pode ser expressa como uma soma de ondas harmônicas de diferentes frequências. (a) Considere a função definida por f x = 4 π c o s x 1
Um fio de 2,00m de comprimento, fixo nas duas extremidades está vibrando em seu modo fundamental. A tração no fiio é de 40,0N e a massa do fio é de 0,100k g . A amplitude no meio do fio é de 2,00c m .
Como você verificou no exercício 15.35, uma onda estacionária descrita pela Equação (15.28) satisfaz a equação de onda, Equação (15.12).a) Mostre que uma onda estacionária descrita pela Equação (15.28
Potência instantânea em uma onda estacionária. De acordo com a Equação (15.21), a taxa instantânea de energia transferida por uma onda ao longo de uma corda ( a potência instantânea) é dada por P x ,
Explique a razão pela qual qualquer onda descrita por uma função da forma y x , t = f ( x - v t ) se desloca no sentido +x com velocidade v .b) Mostre que y ( x , t = f - v t satisfaz à equação de ond