Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 13.4 - Ex. 25
Uma esfera maciça homogênea tem uma massa de e um raio de 1,0 m. Qual é o módulo da força gravitacional exercida pela esfera sobre uma partícula de massa m localizada a uma distância de (a) 1,5 m e (b) 0,50 m do centro da esfera? (c) Escreva uma expressão geral para o módulo da força gravitacional sobre a partícula a uma distância do centro da esfera.
Passo 1
Falaaa galerinha bonita, show de bolinha com vocês?
Saca só, nesse exercício aqui, a gente quer encontrar a força gravitacional que uma esfera maciça de e um raio de exerce sobre uma partícula.
E segundo o teorema de Gauss, se o ponto estiver dentro da esfera a uma distância r do centro, a gente leva em consideração no cálculo da aceleração somente quantidade de massa dentro uma esfera de raio. Se o ponto estiver fora, então a gente leva em consideração a massa total da esfera. Dito isto, a gente já consegue resolver a questão.
Primeiro a gente precisa calcular a densidade da esfera.
A figura a seguir mostra a partícula do lado de fora da esfera
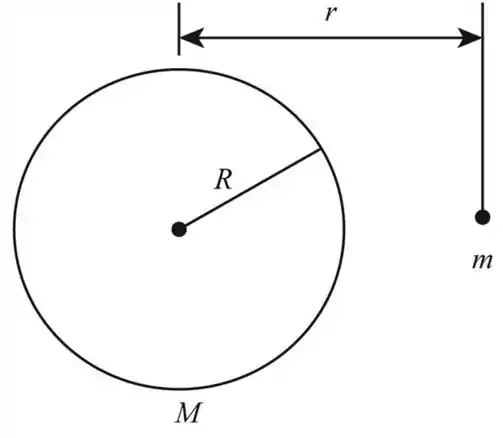
Na letra (a), como o ponto está fora da esfera, a gente leva em consideração a massa total da esfera.
Portanto, a força gravitacional entre a esfera e uma partícula a uma distância de 1.5 m é de
Passo 2
No item (b), só uma parte da esfera que entra na conta. Vamos calcular a massa que está dentro da esfera imaginária de raio 0,50 m.
A figura a seguir mostra a partícula dentro da esfera
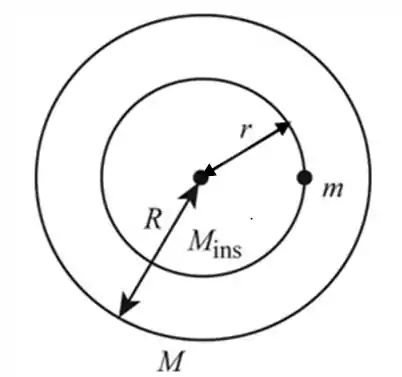
Se uma partícula está localizada dentro de uma esfera sólida uniforme a uma distância r de seu centro, a força gravitacional exercida sobre a partícula é devida apenas à massa que está dentro de uma esfera de raio r.
Passo 3
A expressão para a massa é
Onde,
é a massa da esfera limitada pelo raio r dentro da esfera
é a densidade da esfera.
A expressão para a força gravitacional entre a esfera de massa e uma partícula de massa m localizada dentro da casca.
Onde
está localizada a força gravitacional entre a esfera de massa e uma partícula de massa m localizada dentro da esfera.
Substituindo a equação (1) para reescrever a equação (2).
Logo, a expressão geral para a magnitude da força gravitacional sobre a partícula a uma distância do centro da esfera é .
Passo 4
Reescrevendo a equação (3)
Substituindo
Portanto, a força gravitacional do centro da esfera sobre uma partícula de massa m localizada a uma distância de 0.50 m é de .
Passo 5
No item (c) Reescrevendo a equação (3)
Substituindo
Portanto, uma expressão geral para a magnitude da força gravitacional na partícula a uma distância do centro é de .
Resposta
(a)
(b) .
(c)