Uma esfera de material dielétrico homogêneo com constante dielétrica κ , de raio a , está uniformemente carregada com densidade linear volumétrica de carga ρ .Calcule o vetor campo elétrico E → dentro e fora da esfera.Ache a diferença de potencial V entre o centro e a superfície da esfera.

a ) E → = ρ r 3 k ϵ 0r ^ ( D e n t r o ) a )E → = ρ a 3 3 κ ϵ 0 r 2r ^( F o r a ) b )V = ρ a 2 6 κ ϵ 0

Enunciado

Vamos calcular o campo elétrico dentro via lei de Gauss. Para isso vamos traçar uma superfície gaussiana de raio . Se liga na figura.

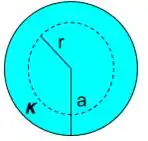
Pela lei de Gauss temos

Como temos um dielétrico o campo fica

Precisamos definir quem é e .

Como estamos dentro da esfera, a carga a ser considerada é situada dentro da superfície gaussiana

Substituindo podemos escrever o campo

O campo aponta para fora na direção radial, portanto

Agora precisamos achar o campo fora, ou seja, . Vamos traçar uma gaussiana fora da esfera

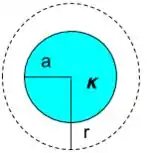
Agora temos

Mas a área é novamente a da superfície gaussiana. Aplicando a lei de Gauss novamente, temos

Novamente o campo está saindo na direção radial

No item (b) ele pede a diferença de potencial entre o centro e a superfície. Precisamos lembrar que

Usando o campo dentro