Enunciado
Física - Moysés - Vol. 3- Ed: 1º - Capítulo 4.Problemas - Ex. 2a
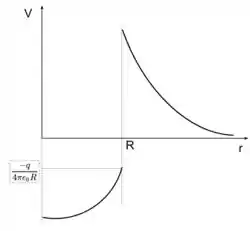
Uma esfera está uniformemente carregada, com carga total . Determine o potencial em pontos internos e externos à esfera e trace um gráfico de em função da distância ao centro.
Passo 1
Se liga! Queremos saber o potencial dentro e fora da esfera, certo?
Então, podemos achar o campo elétrico e depois usá-lo para achar o potencial.
Vamos começar traçando uma gaussiana, tipo essa em vermelho na figura, e depois vamos usar a lei de Gauss.
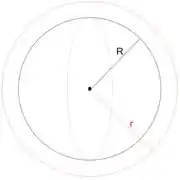
Pela lei de Gauss, o fluxo é dado por
Para uma esfera de raio , temos que é a carga total da esfera, logo
E a área é a área da superfície gaussiana.
Então o campo é
Passo 2
Agora vamos considerar que no infinito o potencial é zero, sendo assim
Passo 3
Para a parte interna da esfera vamos fazer de maneira análoga à parte externa.
Agora a gaussiana está na parte interna, como podemos ver na figura
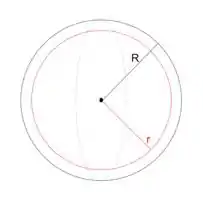
Pela lei de Gauss, o fluxo é dado por
Para uma esfera de raio , temos que é a dentro da gaussiana, logo
E a área é a área da superfície gaussiana.
Então o campo é
Passo 4
Agora vamos considerar que no infinito o potencial é zero, sendo assim
Passo 5
Precisamos montar o gráfico com as funções encontradas.
