Enunciado
Física - Moysés - Vol. 3- Ed: 1º - Capítulo 5.Problemas - Ex. 9
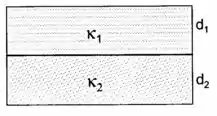
O espaço entre as placas (de área ) de um capacitor plano está preenchido por duas camadas dielétricas adjacentes, de espessuras e e constantes dielétricas e , respectivamente. A diferença de potencial entre as placas é e o campo aponta de 1 para 2. Ache:
- A capacitância do capacitor.
- A densidade superficial de carga livre nas placas.
Passo 1
Podemos escrever que o potencial é
A carga na placa é
Sabendo que
Basta subistituirmos (1) e (2)
Como estão preenchidos por dielétrico, temos
Passo 2
Como temos capacitores em série
Esta é a resposta do item (a).
Passo 3
Agora precisamos achar a densidade superficial. Como já vimos
Mas sabemos que
Portanto
Resposta
Exercícios de Livros Relacionados
Calcule o valor da polarização elétrica à distância r = 10c m do centro de uma pequena esfera metálica possuindo carga de 1,00 ⋅ 10 - 12C , imersa em um meio homogêneo de constante dielétrica κ = 2,00
As faces de uma folha de mica, de espessura igual a 30μ m , são metalizadas para formar um capacitor, como mostra a Figura 18.16.a) Por que uma estreita faixa próxima às bordas é deixada sem metalizaç
O campo elétrico no interior de um meia cuja suscetibilidade elétrica varia na forma χ = a x , onde a é uma constante, é constante, com valor E → = Ei → . Calcule:a) A expressão para a polarização elé
Esboce as linhas de força do campo elétrico referentes à figura 18.18, utilizando as informações dados no Problema 18.6.
A Figura 18.19 mostra uma esfera metálica carregada, incrustada em outra esfera concêntrica contendo duas camadas de materiais dielétricos distintos. Esboce as linhas de campo (a) do campo E → e (b) d