Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 18.Exercícios e Problemas - Ex. 8
A Figura 18.19 mostra uma esfera metálica carregada, incrustada em outra esfera concêntrica contendo duas camadas de materiais dielétricos distintos. Esboce as linhas de campo (a) do campo e (b) do campo .
Passo 1
Nos dois problemas anteriores nós percebemos que para fora da esfera condutora, temos:
Seja o raio da esfera condutora, o raio da segunda esfera e o raio da terceira, temos que
Com isso, as linhas de campo do vetor ficam simplesmente
O vetor não depende do meio!
Passo 2
Para o campo , basta lembrar que
Assim, para :
Para , temos ; para temos e, para , temos :
Com isso, o esboço das linhas fica
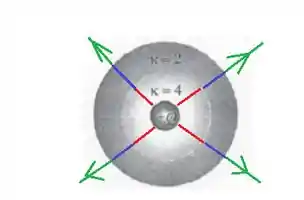
Desenhei em cores diferentes pois os valores do campo mudam em meios diferentes!
Resposta
Desenho.
Exercícios de Livros Relacionados
Você trabalha em uma companhia de engenharia que produz capacitores usados para armazenamento de energia para lasers pulsados. Seu gerente pede à sua equipe para construir um capacitor de placas paral
Um capacitor retangular de placas paralelas tem comprimento a e largura b , e tem um dielétrico de largue b parcialmente inserido até uma distância x entre as placas, como mostra a Figura 24-89. (a) D
Um capacitor eletricamente isolado que tem uma carga Q na sua placa carrega positivamente está preenchido parcialmente com uma substância dielétrica como mostra a Figura 24-49. O capacitor consiste em
Um capacitor de placas paralelas não tem nenhum dielétrico no espaço entre as placas, tem capacitância C 0 e a separação entre as placas é d . Duas lâminas dielétricas que têm constantes dielétricas κ
Nem todos os dielétricos que separam as placas de um capacitor são rígidos. Por exemplo, a membrana de um nervo axônio é uma bicamada de lipídeos que tem uma compressibilidade finita. Considere um cap