Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 13.5 - Ex. 38
No espaço sideral, a esfera , com 20 kg de massa, está na origem de um eixo e a esfera , com 10 kg de massa, está no mesmo eixo em . A esfera é liberada a partir do repouso enquanto a esfera A é mantida fixa na origem. (a) Qual é a energia potencial gravitacional do sistema das duas esferas no momento em que a esfera é liberada? (b) Qual é a energia cinética da esfera após ter se deslocado em direção à esfera .
Passo 1
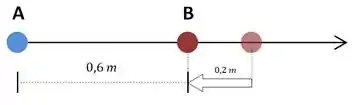
(a) Bom, segundo o enunciado, temos duas esferas dispostas da seguinte forma:
Em primeiro lugar, queremos a energia potencial gravitacional do sistema no momento em que a esfera é liberada. Como estamos no espaço sideral, nosso sistema inclui apenas as duas esferas e , então podemos usar a fórmula para a energia potencial gravitacional entre dois corpos:
Sabemos que, no momento em que é liberada, a distância entre os corpos é . Como já conhecemos as massas e , é só substituir na fórmula para obter:
Lembrando que é a constante gravitacional universal: .
No enunciado, todos os valores têm ao menos 2 algarismos significativos, então devemos deixar nossa resposta dessa forma:
Passo 2
(b) Agora a esfera se deslocou na direção da esfera . Queremos então saber a energia cinética da esfera após esse deslocamento:
Uma dica: se estamos discutindo a energia em um sistema que sofre alguma mudança, provavelmente teremos que aplicar a lei de conservação de energia! E é isso que faremos para resolver essa questão.
Essa lei dá a seguinte igualdade:
Onde é a energia cinética e é a energia potencial. Queremos obter .
Como a esfera parte do repouso, temos , e já encontramos no item (a):
Para podermos encontrar falta apenas achar o .
Pra isso é só fazer a mesma coisa do item (a)! A única coisa que muda é a distância , que agora vale .
Substituindo na lei de conservação de energia:
Resolvendo a equação e ajustando novamente os algarismos significativos:
Pronto!
Resposta
(a)
(b)