Enunciado
Física - Moysés - Vol. 3- Ed: 1º - Capítulo 7.Problemas - Ex. 4
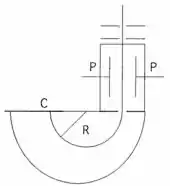
No espectrógrafo de massa de Bainbridge (fig.), há um campo elétrico uniforme E e um campo magnético uniforme B perpendicular ao plano da figura na região entre as placas PP, ajustados de modo a formar um filtro de velocidades, ou seja, só deixar passar íons de velocidade bem definida para a região semicircular inferior, onde existe um outro campo uniforme B’ também perpendicular ao plano da figura. Mostre que, para íons de carga , o raio da órbita semicircular é proporcional à massa do íon, de forma que a placa fotográfica registra um espectro de massa, em que a distância ao longo da chapa é proporcional à massa do íon.
Passo 1
Se liga! Aqui precisamos prestar atenção que o campo magnético deve produzir uma força de mesma intensidade que o campo elétrico. Portanto, temos
Passo 2
Para o item no trecho onde a trajetória é semicircular, temos que durante essa parte existirá uma resultante centrípeta provocada pela força produzida pelo campo magnético B’. Então podemos escrever que
Como já vimos que
Substituindo os valores q pela carga d o elétron, temos