Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 1.Problemas - Ex. 58
Duas cordas em um plano vertical exercem as mesmas forças de módulo sobre um peso suspenso, mas a tração entre elas possui um ângulo de . Qual é a força de tração que cada uma exerce, se a tração resultante é de 372 N diretamente para cima?
Passo 1
E aiii galera!
Tudo bom com vocês?
Vamos fazer mais uma questãozinha?
Bom... o enunciado nos diz que duas cordas em um plano vertical exercem as mesmas forças de módulo sobre um peso suspenso, mas a tração entre elas possui um ângulo de .
Queremos calcular a força de tração que cada uma exerce, se a tração resultante é de diretamente para cima.
Para resolvermos isso, temos que decompor os vetores e somar cada componente, belezinha?
Passo 2
Os dois vetores e sua resultante são mostrados na figura abaixo e :
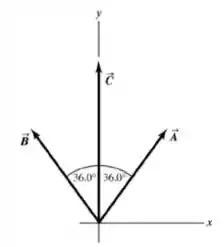
Passo 3
Então,
A soma das magnitudes das duas forças excede a magnitude da força resultante porque apenas um componente de cada força é para cima.