Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 6.Problemas Adicionais - Ex. 71
Uma locomotiva acelera um trem de 25 vagões em uma linha férrea plana. Cada vagão possui uma massa de e está sujeito a uma força de atrito , onde a velocidade está em metros por segundo e a força está em newtons. No instante em que a velocidade do trem é , o módulo da aceleração é . (a) Qual é a tensão no engate entre o primeiro vagão e a locomotiva? (b) Se essa tensão é igual à força máxima que a locomotiva pode exercer sobre o trem, qual é o maior aclive que a linha férrea pode ter para que a locomotiva consiga puxar o trem a ?
Passo 1
Então galera , podemos tratar os 25 vagões como um único objeto de massa , e como já conhecemos sua velocidade() , podemos obter a força de atrito através da relação :
Considerando a força de tração exercida pela locomotiva e usando a Segunda Lei de Newton, temos que :
Passo 2
Agora podemos construir o diagrama de corpo livre do conjunto de vagões, na qual é o ângulo entre a força resultante e a força peso . Escolhemos um eixo encosta acima (na direção do canto superior direito da figura).
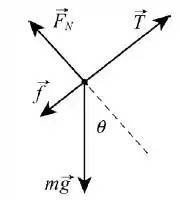
Aplicando a Segunda Lei de Newton ao eixo x, temos:
Fazendo e substituindo , e pelos valores que já conhecemos , obtemos
Resposta
Tranquilo pessoal? Bora resolver mais questões então