Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 40
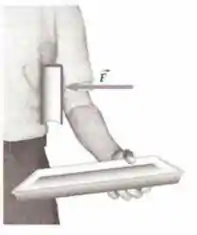
Um estudante de física cansado e sobrecarregado tenta manter um grande livro de física preso com seu braço, como mostra a Figura abaixo. O livro tem uma massa de . O coeficiente de atrito estático entre o livro e o antebraço do estudante é 0,320 e o coeficiente de atrito estático entre o livro e a camisa do estudante é (a) Qual é a força horizontal mínima que o estudante deve aplicar ao livro para evitar que ele caia? (b) Se o estudante só pode exercer uma força de , qual é a aceleração do livro ao escorregar de sob seu braço? O coeficiente de atrito cinético do braço contra o livro é e o da camisa contra o livro é .
Passo 1
Item (a)
Nós podemos usar a 2° Lei de Newton para calcular a força mínima horizontal que o aluno terá que realizar para segurar o livro. Abaixo, vemos o diagrama de forças que estão presentes no livro:
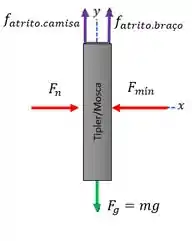
Nesse diagrama, é a força mínima que o braço do estudante tem que fazer para segurar o livro e é a força normal de contato entre a superfície da camisa do estudante e o livro.
E as forças que estão apontando para cima são as forças de atrito do livro com a camisa e com o braço do estudante, da mesma forma que a força que está apontando para baixo é o peso do livro.
Vamos ver como a gente acha essa força mínima que o estudante deve aplicar no livro!
Passo 2
Assumindo o eixo x e o eixo y que estão no diagrama, como o livro está em equilíbrio (paradinho), temos e . Por isso, pela segunda lei de Newton vale que:
Através dessa equação, vemos que .
Agora para o eixo , lembrando que a segunda lei de Newton fica:
Como
Passo 3
Agora vamos parar para pensar. Qual é a expressão de e ?
Se a gente quer a força mínima do estudante para segurar o livro, essas forças de atrito devem ser máximas. E como o livro está parado, temos atrito estático máximo.
E qual é a expressão dele? É essa aqui:
Onde é o coeficiente de atrito estático entre duas superfícies. O enunciado deu essa informação para o contato entre a camisa do estudante e o livro , e para o contato entre o antebraço do estudante e livro .
E a força normal é a força normal entre a camisa e o livro, que vimos que é . Então a expressão dos nossos atritos é:
Passo 4
Substituindo essas duas coisas em :
Isolando quem a gente quer
Substituindo pelos valores numéricos que já temos:
Passo 5
Item (b) O diagrama de forças é o mesmo da letra anterior, mas agora as forças não vão se cancelar no eixo y, porque há uma aceleração diferente de zero.
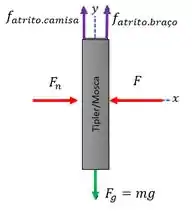
Então precisamos aplicar a segunda lei de Newton para achar , que é o que ele pede. Fica assim:
Como
Agora há movimento na direção do atrito, então essas forças são de atrito cinético, que é dado pela fórmulinha:
Onde é o coeficiente de atrito cinético, e enunciado dá ele para as duas superfícies em contato com o livro.
De acordo com a 2° Lei de Newton, como o livro não desloca para os lados, apenas para baixo, sabemos que as forças horizontais são iguais e chamaremos elas de , já que é a força na horizontal aplicada pelo estudante.
Então a expressão dos nossos atritos é:
Passo 6
Substituindo essas duas coisas em :
Sendo a aceleração com que o livro cai, então:
Substituindo pelos valores numéricos que já possuímos:
O sinal de negativo indica que a aceleração é contrária ao eixo y, isto é, para baixo.
Resposta
, para baixo.