Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 6.1 - Ex. 5
Dê um exemplo de uma partícula que tem energia cinética constante mas está acelerada. Pode uma partícula não acelerada ter energia cinética variável? Caso afirmativo, dê um exemplo.
Passo 1
Cara, ele quer o exemplo de uma partícula com energia cinética constante mas que está acelerada, ou seja, que tem aceleração não nula.
Vamos lembrar da expressão da energia cinética:
Percebe que ela depende da massa da partícula que é sempre constante e da rapidez da partícula.
Então para ser constante, precisamos que a rapidez da partícula seja constante.
Ou seja, a gente quer um exemplo onde a rapidez da partícula seja constante mas essa partícula tem uma aceleração.
Passo 2
Agora pensando num caso onde temos rapidez constante mas temos aceleração, a gente pode pensar em um movimento circular de rapidez constante!
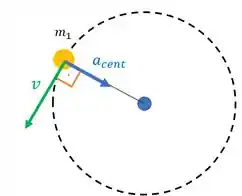
Por que?
Porque temos a aceleração centrípeta (gerada pela força centrípeta) atuando sobre a partícula. Essa força centrípeta é o que mantem a partícula em um movimento de trajetória circular.
E nesse caso, a aceleração é sempre perpendicular a velocidade, por isso ela não muda a magnitude da velocidade (rapidez). Ela muda somente a direção dessa velocidade.
Assim temos rapidez constante, logo, energia cinética constante.
Passo 3
Cara, o papel da aceleração é modificar o vetor velocidade. Ela pode modificar a magnitude, o sentido ou a direção do vetor velocidade.
Ou seja, se houve mudança da magnitude da velocidade, ou seja, mudança na rapidez, é porque houve ação da aceleração.
Se não houver aceleração, não há quem mude a rapidez. Logo, temos rapidez constante.
Vimos no passo 1 que se a rapidez for constante, então a energia cinética também é.
Logo, não podemos ter energia cinética variável sem aceleração, porque isso implica não ter variação na rapidez da partícula.
Resposta
Uma partícula se movendo circularmente com velocidade constante.
Não.