Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 7.Problemas - Ex. 1
No Exemplo 1 da Seç. 5.3, considere a situação em que |F| tem o valor mínimo necessário para manter o bloco desliando sobre o plano horizontal com velocidade constante. Para um deslocamentodo bloco, exprima o trabalho W realizado pela força F em função de e do coeficiente de atrito . Que acontece com esse trabalho?
Passo 1
A primeira coisa a se perceber é que
Vamos desenhar o diagrama e analisar as componentes
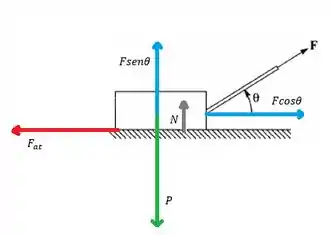
- Na horizontal
- Na vertical
Juntando agora as duas equações fica assim
Ok, vamos calcular o trabalho realizado pela força F sobre o bloco
Passo 2
Todo esse trabalhão e nosso corpo nem acelera, mas por que? Todo o trabalho é dissipado pela força de atrito, então na medida que o corpo ganha energia também perde, show!
Resposta
O trabalho do peso é dissipado pelo trabalho do atrito
Exercícios de Livros Relacionados
Uma força resultante ao longo do eixo x , com componente F x = - 12,0N + 0,300N / m 2x 2 é aplicada a um objeto de 5,00k g que se encontra inicialmente na origem e movendo-se na direção x negativa com
Uma extremidade de uma mola horizontal com constante de força igual a 130,0N / m é presa a uma parede vertical. Um bloco de 4,00k g apoiado sobre o piso é colocado contra a mola. O coeficiente de atri
A Figura P6.90 mostra os resultados que a medição da força F exerceu sobre as duas extremidades de uma tira elástica para esticá-la a uma distância x de sua posição em repouso. Os pontos de dados estã
A Fig. 7-39 mostra a aceleração de uma partícula de 2,00k g sob a ação de uma força F que desloca a partícula ao longo de um eixo x , a partir do repouso, de x=0 a x=9,0m . A escala vertical do gráfic
Suponha que o trenó do Exercício 6.24 esteja inicialmente em repouso em x= 0. Use o teorema do trabalho-energia para achar velocidade a do trenó em a) x= 8,0 m; b) x = 12,0 m. Despreze o atrito entre