O Exemplo 12.2 (Seção 12.1) mostra que a aceleração de cada esfera produzida pela força gravitacional é inversamente proporcional à massa da respectiva esfera. Então, como você explica que qualquer corpo caindo nas vizinhanças da superfície terrestre possui a mesma aceleração da gravidade?

Faaaaala meu povo, bora iniciar mais um livrinho com a gente!

Se liga que essa questãozinha nos pede para analisar a afirmação do nosso querido estudante.

Podemos tratar este problema em 1 dimensão. Vamos rotular o centro de massa da Terra por e a posição do observador por (onde é o raio da terra) e o objeto que está caindo em direção à Terra. Para simplificar vamos considerar . Em seguida, definimos a distância do objeto em queda do observador:

Suponha que a Terra e o objeto em queda estejam a uma certa distância e a magnitude do par de forças é , então a aceleração relativa é dada por:

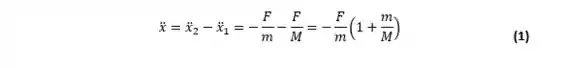
Onde e são massas do objeto em queda e da Terra. A magnitude da força varia com a distância, mas é a mesma para todos os objetos. A partir da equação 1, é fácil ver que a correção é desprezível na experiência cotidiana, pois .

Te ajudei? Belezinha, até a próxima então!