Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 5.9 - Ex. 21
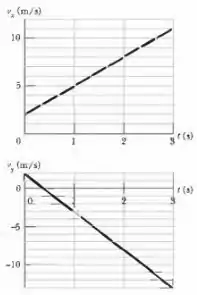
Uma força horizontal constante empurra um pacote dos correios de sobre um piso sem atrito onde um sistema de coordenadas foi desenhado. A Fig. 5-37 mostra as componentes e da velocidade do pacote em função do tempo . Quais são (a) o módulo e (b) a orientação de ? Ver Fig. 5-37, adiante.
Passo 1
Para iniciar a resolução deste problema precisamos ter em mente que a força resultante que age sobre um corpo é a soma de todas as forças que atuam no mesmo e está relacionada à aceleração pela definição da segunda lei de Newton:
Lembrando que podemos aplicar a segunda lei de Newton separadamente para cada componente, assim:
E o ângulo medido em relação ao semieixo positivo é dado por:
Sem esquecer que para calcular o módulo de um vetor, usamos a seguinte equação:
Além disso, para resolver esta questão precisamos lembrar que para um movimento com aceleração constante, a aceleração média é igual a aceleração instantânea e, por isso:
O problema, além de nos informar a massa do corpo (), nos dá dois gráficos de velocidade em função do tempo, um referente ao eixo e outro ao eixo . A partir deles, determinaremos o módulo da força resultante e também a orientação da mesma.
Passo 2
Vamos iniciar essa questão calculando a componente da aceleração usando a equação da aceleração média com os dados extraídos do gráfico.
Considerando os pontos e :
Prosseguindo, de maneira análoga, para a componente da aceleração. Para este, consideraremos os pontos e :
Passo 3
Com os valores das componentes da aceleração já calculados, vamos partir para aplicação direta da segunda lei de Newton para cada eixo, vamos lá? Foca aqui que já está terminando
A segunda lei de Newton para o eixo :
Para o eixo :
Passo 4
Para determinar o módulo do vetor usaremos a equação dada no passo inicial:
Passo 5
Por fim, usaremos a equação também enunciada no passo inicial para determinar o ângulo que o vetor da força resultante faz com o semieixo positivo:
Devemos tomar cuidado quando utilizando a função na calculadora, pois dois ângulos e possuem o valor. Assim, precisamos determinar em qual quadrante o nosso vetor está a partir da análise do sinal das componentes.
Como nosso vetor possui a componente positiva e a componente negativa, então este só pode estar no quarto quadrante, pois é o único cujo o seno é negativo e cosseno é positivo, portanto:
Resposta
- ;
- .