Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 3.Exercícios e Problemas - Ex. 3
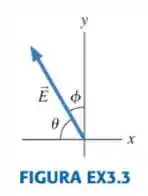
- Quais são os componentes e do vetor em termos do ângulo e do módulo E mostrados na FIGURA EX3.3?
- Para o mesmo vetor, quais são os componentes e em termos do ângulo e do módulo E?
Passo 1
Para resolver essa questão precisamos lembrar como decompor um vetor de acordo com o ângulo que ele forma:
Nós iremos decompor um vetor em duas componentes, uma na direção do eixo e outra na direção do eixo como na Figura:
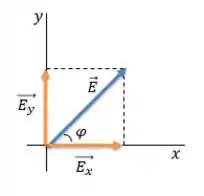
E o valor de cada componente, em função do ângulo fica assim:
A componente que está COlada com o ângulo é igual ao módulo do vetor vezes o COsseno do ângulo. Já a componente que está SEparada do ângulo é igual ao módulo do vetor vezes o SEno do ângulo.
Pegou o macete?
Passo 2
Agora que já relembramos como decompor o ângulo podemos resolver o problema.
Vamos separar o vetor dado na Figura EX3.3 em duas componentes:
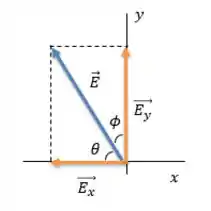
Passo 3
- Quais são os componentes e do vetor em termos do ângulo e do módulo E mostrados na FIGURA EX3.3?
- Para o mesmo vetor, quais são os componentes e em termos do ângulo e do módulo E?
Agora vamos achar o valor das componentes em função do ângulo , como está nos pedindo a letra a.
A componente está colada no ângulo e a componente está separada do ângulo . Então:
Nota que para a componente tem um sinal de negativo acompanhando. Esse sinal é pra indicar que essa componente está apontando no sentido contrário ao sentido do eixo . Beleza?
Passo 4
Agora vamos achar o valor das componentes em função do ângulo , como está nos pedindo a letra b.
A componente está separada do ângulo e a componente está colada no ângulo . Então:
Novamente a componente tem um sinal de negativo acompanhando, porque esse sinal indica que essa componente está apontando no sentido contrário ao sentido do eixo . Beleza?
Resposta
- ;
- ;