Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 4- Ed: 10º - Capítulo 36.1 - Ex. 6

Um feixe de luz com um comprimento de onda de 441 nm incide em uma fenda estreita. Em uma tela situada a 2,00 m de distância, a separação entre o segundo mínimo de difração e o máximo central é 1,50 cm. (a) Calcule o ângulo de difração θ do segundo mínimo. (b) Determine a largura da fenda.

Passo 1

Nesse exercício vamos utilizar a equação para o mínimo de difração, isolando o ângulo θ para encontrar o ângulo de difração. Após isso vamos calcular o tamanho da fenda para um m qualquer.

Passo 2

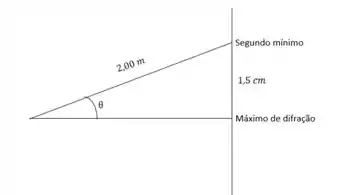
Podemos notar por essa linda esquematização do autor dessa resolução, que o ângulo θ pode ser obtido pela relação trigonométrica do seno, assim

θ = sin - 1 ⁡ 0,015   m 2,00   m = 0,430 °

Passo 3

Temos que a relação para os mínimos de difração é dada por a ⋅ sin ⁡ θ = m ⋅ λ . Podemos então isolar a largura de fenda a e substituir os valores que temos para resolver o problema. Assim, chegamos na seguinte relação

a = m ⋅ λ sin ⁡ θ

Usando nosso m = 2 , já que temos o ângulo para o segundo mínimo de difração, chegamos que

a = 2 ⋅ 441 × 10 - 9   m sin ⁡ 0,430 ° ≅ 0,118   m m

Resposta

  1. θ = 0,430 °
  2. a ≅ 0,118   m m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A Fig. 36-38 mostra a variação do parâmetro α da Eq. 36-6 com o seno do ângulo θ em um experimento de difração de fenda única usando uma luz com um comprimento de onda de 610 nm. A escala do eixo vert
Uma luz monocromática com um comprimento de onda de 538 nm incide em uma fenda com 0,025 mm de largura. A distância entre a fenda e a tela é 3,5 m. Considere um ponto da tela situado a 1,1 cm de distâ
No experimento de difração de fenda única da Fig. 36-4, suponha que o comprimento de onda da luz é 500 nm, a largura da fenda é 6,00μ m e a tela de observação está a uma distância D = 3,00m . Defina o
Mostre que os valores de α para os quais a intensidade da figura de difração de uma fenda é máxima podem ser determinados exatamente derivando a Eq. 36-5 em relação a α e igualando o resultado a zero,
A largura total a meia altura (LTMA) de um máximo central de difração é definida como o ângulo entre os dois pontos nos quais a intensidade é igual à metade da intensidade máxima. (Veja a Fig. 36-8b.)