Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 4- Ed: 10º - Capítulo 36.2 - Ex. 13

Uma luz monocromática com um comprimento de onda de 538 nm incide em uma fenda com 0,025 mm de largura. A distância entre a fenda e a tela é 3,5 m. Considere um ponto da tela situado a 1,1 cm de distância do máximo central. Calcule (a) o valor de θ nesse ponto, (b) o valor de α e (c) a razão entre a intensidade nesse ponto e a intensidade do máximo central.

Passo 1

Nesse exercício vamos usar uma relação trigonométrica para descobrir qual o ângulo do ponto P como também usar as relações para 36-6 e 36-5 para calcularmos a intensidade no mesmo ponto.

Passo 2

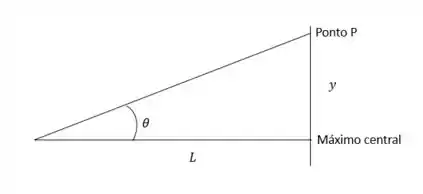
  1. A situação descrita pelo enunciado é da forma mostrada na imagem acima (confia). Dessa forma, podemos descobrir o ângulo θ através do valor de sua tangente. Assim, temos que

    2. θ = tan - 1 ⁡ y L = tan - 1 ⁡ 0,011   m 3,5   m = 0,18 º

    Passo 3

  2. Temos pela relação 36-6 que α pode ser obtido da seguinte forma

    3. α = π ⋅ a λ ⋅ sin ⁡ θ

    Substituindo os valores dados pelo problema, temos que

    α = π ⋅ 0,025 × 10 - 3   m ⋅ sin ⁡ 0,18 º 538 × 10 - 9   m = 0,46   r a d

    Passo 4

  3. Usando agora a equação 36-5, temos que a intensidade que chega no ponto P pode ser dada pela equação

I θ I m = sin ⁡ α α 2 = sin ⁡ 0,46 0,46 2 = 0,93

Resposta

  1. θ = 0,18 º
  2. α = 0,46   r a d
  3. I θ I m = 0,93
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os fabricantes de fios (e outros objetos de pequenas dimensões) às vezes usam um laser para monitorar continuamente a espessura do produto. O fio intercepta a luz do laser, produzindo uma figura de di
Uma fenda com 1,00 mm de largura é iluminada com uma luz cujo comprimento de onda é 589 nm. Uma figura de difração é observada em uma tela situada a 3,00 m de distância da fenda. Qual é a distância en
O Princípio de Babinet. Um feixe de luz monocromática incide perpendicularmente em um furo “colimador” de diâmetro x ≫ λ . O ponto P está na região de sombra geométrica, em uma tela distante (Fig. 36-
Uma fenda de 0,10 mm de largura é iluminada com uma luz cujo comprimento de onda é 589 nm. Considere um ponto P em uma tela na qual a figura de difração é observada; o ponto está a 30º do eixo central
A Fig. 36-38 mostra a variação do parâmetro α da Eq. 36-6 com o seno do ângulo θ em um experimento de difração de fenda única usando uma luz com um comprimento de onda de 610 nm. A escala do eixo vert