Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 4- Ed: 10º - Capítulo 36.2 - Ex. 12

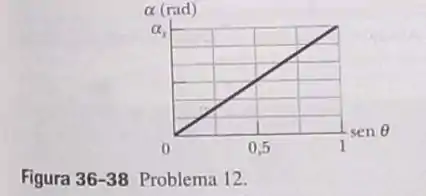
A Fig. 36-38 mostra a variação do parâmetro α da Eq. 36-6 com o seno do ângulo θ em um experimento de difração de fenda única usando uma luz com um comprimento de onda de 610 nm. A escala do eixo vertical é definida por α s = 12   r a d . Determine (a) a largura da fenda, (b) o número total de mínimos de difração (dos dois lados do máximo central), (c) o menor ângulo para o qual existe um mínimo e (d) o maior ângulo para qual existe um mínimo.

Passo 1

Nesse exercício vamos fazer uma análise do gráfico e utilizar as Eq. 36-6 além da equação para os mínimos de difração para encontrarmos a quantidade máxima de mínimos que existem nessa difração

Passo 2

  1. Temos que esse gráfico é dado por α × sin ⁡ θ , ou seja, α em função do sin ⁡ θ . Assim, temos que a equação que rege essa curva é dada por

    2. α = π ⋅ a λ ⋅ sin ⁡ θ

    Pegando o ponto (1,12), onde sin ⁡ θ = 1 e α = 12   r a d , temos que a largura de nossa será

    a = 12   r a d ⋅ 610 × 10 - 9   m π ⋅ 1 = 2,33 × 10 - 6   m

    Passo 3

  2. Usando a relação para os mínimos de difração, temos que a ⋅ sin ⁡ θ = m ⋅ λ . Como queremos a quantidade máxima de mínimos, temos que que será preciso utilizar o valor de sin ⁡ θ m á x . Portanto, temos que isolando m m á x e substituindo os valores, vamos chegar em

    3. m m á x = a ⋅ sin ⁡ θ m á x λ = 2,33 × 10 - 6   m 610 × 10 - 9   m = 3,82

    Isso nos diz que existem 3 mínimos de cada lado, totalizando 6 mínimos de difração, pois para m apenas se admite números inteiros.

    Passo 4

  3. Utilizando a mesma relação para os mínimos de difração, mas agora isolando θ e admitindo m = 1 , teremos que

    4. θ m í n = sin - 1 ⁡ λ a = sin - 1 ⁡ 610 × 10 - 9   m 2,33 × 10 - 6   m = 15,2 º

    Passo 5

  4. Da mesma forma que no item anterior, mas agora para m = 3 , teremos que

θ m á x = sin - 1 ⁡ 3 ⋅ λ a = sin - 1 ⁡ 3 ⋅ 610 × 10 - 9   m 2,33 × 10 - 6   m = 51,8 º

Resposta

  1. a = 2,33 × 10 - 6   m
  2. m m á x = 6 Mínimos
  3. θ m í n = 15,2 º
  4. θ m á x = 51,8 º
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um feixe de luz com um comprimento de onda de 441 nm incide em uma fenda estreita. Em uma tela situada a 2,00 m de distância, a separação entre o segundo mínimo de difração e o máximo central é 1,50 c
Uma fenda é iluminada por um feixe de luz que contém os comprimentos de onda λ a e λ b , escolhidos de tal forma que o primeiro mínimo de difração da componente λ a coincide com o segundo mínimo da co
Uma onda plana com um comprimento de onda de 590n m incide em uma fenda de largura a=0,40 mm. Uma lente convergente delgada de distância focal + 70c m é colocada entre a fenda e uma tela de observação
Um feixe de luz com um comprimento de onda de 633 nm incide em uma fenda estreita. O ângulo entre o primeiro mínimo de difração de um lado do máximo central e o primeiro mínimo de difração do outro la
Ondas sonoras com uma frequência de 3000 Hz e uma velocidade de 343 m/s passam pela abertura retangular de uma caixa de som e se espalham por um grande auditório de comprimento d = 100m . A abertura,