Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 15.Problemas Adicionais - Ex. 79

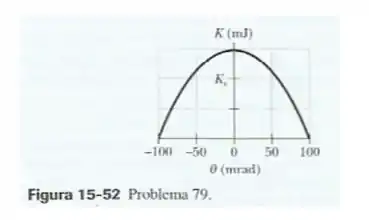
A Fig. 15-52 mostra a energia cinética K de um pêndulo simples em função do ângulo θ com a vertical. A escala do eixo vertical é definida por K = 10,0 m J . O peso do pêndulo tem uma massa de 0,200 k g . Qual é o comprimento do pêndulo?

Passo 1

Fala galerinha bonita, tudo beleza?

Nesse exercício aqui, o gráfico mostra a energia cinética K de um pêndulo simples em função do ângulo θ com a vertical. E sabendo que a escala do eixo é definida por K = 10,0   mJ e que o peso do pêndulo tem uma massa de 0,200   kg , o enunciado quer que a gente encontre o comprimento do pêndulo.

Se a escala do eixo vertical vale K = 10,0   mJ , a gente percebe que a energia cinética máxima:

K m a x = 15   mJ

K m a x = 0,015   J

Logo, podemos calcular a velocidade máxima do pêndulo neste ponto:

K m a x = 1 2 m v m a x 2 = 0,015   J

Isolando a velocidade, obtemos que:

v m a x = 2 0,015 m

v m a x = 0,387 m / s

Então, podemos calcular a o comprimento do pêndulo através da equação abaixo:

v m a x = 2 g L 1 – cos ⁡ θ m a x

Invertendo para obter o valor L , nós temos que:

L = v m a x 2 2 g 1 - c o s θ

L = 1,53   m

Resposta

L = 1,53   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Qual será o período do pendulo do Problema 60 se o pendulo estivesse na lua, onde a aceleração da gravidade é um sexto a da Terra?
Mostre que a energia total de um pêndulo simples sob oscilações de pequena amplitude ϕ 0 (em radianos) é E ≈ 1 2 m g L ϕ 0 2 . Dica: Use a aproximação c o s ϕ ≈ 1 - 1 2 ϕ 2 para pequenosϕ .
Um pêndulo simples de comprimento L é preso a um carrinho de grande massa que desliza sem atrito por um plano inclinado em um ângulo θ com a horizontal, como mostra a Figura 14-28. Encontre o período
A massa no final de um pêndulo simples de comprimento L é liberada do repouso a partir de um ângulo ϕ 0 . (a) Modele o movimento do pêndulo como movimento harmônico simples e encontre sua velocidade a
Qual é o comprimento de um pêndulo simples no qual o peso leva 3,2s para descrever uma oscilação completa?