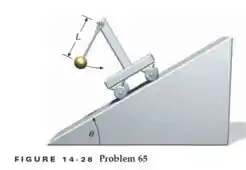
Um pêndulo simples de comprimento L é preso a um carrinho de grande massa que desliza sem atrito por um plano inclinado em um ângulo com a horizontal, como mostra a Figura 14-28. Encontre o período de oscilação para pequenas oscilações deste pêndulo.

Essa aceleração pode ser escrita como a soma da aceleração da massa em relação ao carrinho com a aceleração do carrinho em relação ao plano :

Substituindo na equação do Passo 1:

Rearranjando os termos:

E essa será a segunda Lei de Newton para a massa no referencial do carrinho, que está acelerado.

O termo entre parênteses será um novo vetor, que chamaremos de gravidade efetiva

Agora vamos dar uma olhada no esquema abaixo dos três vetores que escrevemos acima:

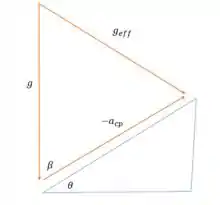
A gravidade efetiva será igual a soma do vetor da gravidade com o oposto da aceleração do carrinho em relação ao plano, já que o carrinho está descendo, então o vetor aponta para cima.

Pela lei dos cossenos, podemos calcular o valor da gravidade efetiva, mas antes podemos escrever como:

E a gravidade efetiva será:

Como e são complementares, , então:

E então:

Agora que temos a gravidade efetiva, basta escrevermos a Segunda Lei de Newton em termos da variável angular e o problema torna-se unidimensional. A tração será zero, pois a força é sempre paralela ao fio do pendulo, não produzindo variação angular e a aceleração tangencial pode ser escrita em termos do comprimento do pendulo e da segunda derivada do ângulo:

A Segunda Lei de Newton então fica:

E o termo aparece pela projeção do vetor da gravidade efetiva com a direção perpendicular ao fio (que causará o movimento do pêndulo)

Como está em ângulos pequenos, . Então:

Reescrevendo:

Que é a equação de movimento harmônico simples.

Dela podemos tirar o :

E então calcularmos o período de oscilações: