Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 14.1 - Ex. 64
Mostre que a energia total de um pêndulo simples sob oscilações de pequena amplitude (em radianos) é . Dica: Use a aproximação para pequenos.
Passo 1
Bom, sabemos que a energia do sistema é dada apenas pela energia potencial e pela energia cinética do pêndulo. Vamos ilustrar a situação para podermos moldar a equação da maneira que o enunciado pede para a gente:
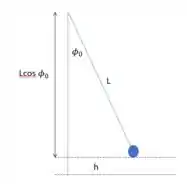
Como podemos ver, o comprimento do pêndulo é L, e a diferença de alturas quando o pêndulo está no extremo, onde o ângulo é , será chamada de h. Podemos escrever h da seguinte forma:
foi determinado pelo triangulo retângulo na imagem.
Passo 2
Quando o pendulo está no extremo, a energia cinética é zero, e então podemos escrever toda a energia mecânica total somente em função da energia potencial:
Que nesse caso é somente a energia potencial gravitacional:
Passo 3
Agora precisamos só substituir h:
E como o enunciado diz que é para ângulos pequenos, e nos dá a seguinte aproximação para esse caso:
Ficamos com:
Que é o que o enunciado pede para mostrar.
Resposta
Ei, a resposta está no passo a passo :)