Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 14.1 - Ex. 66
A massa no final de um pêndulo simples de comprimento L é liberada do repouso a partir de um ângulo . (a) Modele o movimento do pêndulo como movimento harmônico simples e encontre sua velocidade ao passar por usando a aproximação de ângulos pequenos. (b) Usando a conservação de energia, encontre essa velocidade exatamente para qualquer ângulo (não apenas pequenos ângulos). (c) Mostre que seu resultado do item (b) concorda com a resposta aproximada na Parte (a) quando é pequeno. (d) Encontre a diferença entre os resultados aproximados e exatos para e . (e) Encontre a diferença entre os resultados aproximado e exato para e
Passo 1
Como a massa é liberada do repouso em , ele será a amplitude do nosso movimento harmônico. Sabemos que a velocidade pode ser escrita em termos da velocidade angular como:
Podemos escrever em termos da amplitude e do tempo:
E a derivada dele será:
A equação da velocidade então fica:
E a velocidade será máxima quando , ou seja, quando logo:
E escrevendo a velocidade angular da seguinte maneira:
Ficamos com:
Passo 2
Para a letra (b) vamos usar a conservação de energia em dois pontos, onde a e energia cinética é máxima e o outro onde a energia potencial é máxima:
E ficamos com:
Observando a imagem abaixo, podemos perceber que a altura h pode ser escrita em termos da diferença entre o comprimento do fio quando ele estivesse em repouso com o comprimento quando ele está na posição de amplitude :
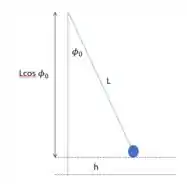
h então será:
Substituindo na equação da velocidade máxima:
Passo 3
Quando é pequeno, podemos fazer , e substituir na equação da velocidade máxima do passo 2:
Que ficará:
Que é o mesmo resultado do Passo 1, o que responde a letra (c).
Passo 4
Vamos agora responder a (d), basta fazermos a diferença entre a aproximação e o valor exato da velocidade máxima e então fazemos a razão dessa diferença pelo valor exato para sabermos se o desvio entre as duas maneiras de resolvermos é grande:
Substituindo os valores:
E a razão será:
Passo 5
A letra (e) pede apenas para mudarmos os valores na equação da velocidade, e compararmos novamente os dois casos, vamos calcular então :
E a razão: