Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 23.8 - Ex. 37
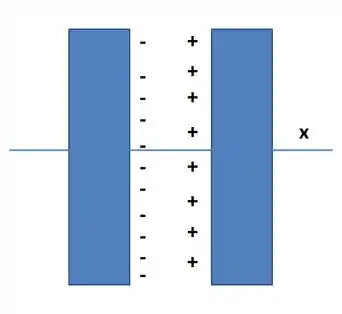
Na Fig. 23-40, duas placas finas , de grande extensão, são mantidas paralelas e uma pequena distância uma da outra. Nas faces internas, as placas possuem densidades superficiais de cargas de sinais opostos e valor absoluto . Em termos dos vetores unitários, determine o campo elétrico (a) à esquerda das placas; (b) à direita das placas; (c) entre as placas.
Passo 1
Falaaaaa galerinhaaa !!
Vamo que vamooo !!
Bom, para o campo elétrico para a placa nós temos uma fórmula:
Onde é a densidade das cargas superficiais da placa.
Vamos lembrar que o campo elétrico causado por cargas negativas convergem para essas cargas, enquanto que o causado por cargas positivas são do tipo divergente.
Passo 2
Dito isso, os campos ocasionados por cada uma das superfícies infinitas e carregadas são dessa forma:
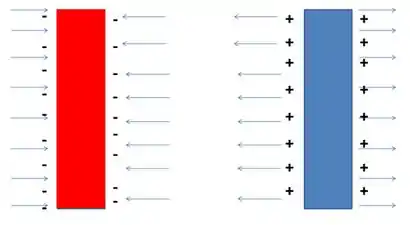
Então, no lado esquerdo nós temos a placa vermelha exercendo um campo elétrico direcionado para o eixo positivo de enquanto o o campo elétrico devido à placa azul está direcionado para o eixo negativo de
Se o campo total é dado por:
Substituindo com a fórmula que achamos?
Não se esqueçam que esse significa na direção do positivo e negativo .
Passo 3
E agora nós vamos para a letra (b) !!
Quando analisamos a direita das placas, a vermelha terá ahora um campo direcionado para o eixo negativo de enquanto para a placa azul terá seu campo direcionado para o lado positivo. O oposto do anterior, não é?
Vamos fazer a mesma coisa que no Passo 1:
Passo 4
E agora só nos resta a letra (c) !!
No interior das placas ambos os campos estão direcionados para o eixo negativo de
Sabendo que:
Só precisamos substituir:
E é isso aí galerinhaa !! Chegamos ao fim de mais umaa !!!