Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 27.7 - Ex. 48

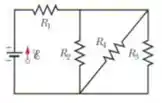
Na Fig. 27-51, R 1 = 7,00 Ω , R 2 = 12,0 Ω , R 3 = 4,00 Ω e a força eletromotriz da fonte ideal é ε = 24,0 V . Determine para que valor de R 4 a potência fornecida pela fonte aos resistores é igual (a) a 60,0 W ; (b) ao maior valor possível P m á x ; ( c) ao menor valor possível P m i n . Determine (d) P m á x ; (e) P m i n .

Passo 1

E aí! como vai? 😎

Nesse problema temos um circuito onde R 2 , R 3 e R 4 estão em paralelo e a equivalência desses resistores está em série com R 1 . Se R 1 = 7,00 Ω , R 2 = 12,0 Ω , R 3 = 4,00 Ω e ε = 24,0 V , nosso objetivo é obter o valor de R 4 de modo que a potência fornecida pela fonte aos resistores é igual (a) a 60,0 W ; (b) ao maior valor possível P m á x ; (c) ao menor valor possível P m i n e tambem queremos determinar (d) P m á x ; (e) P m i n .

Tem ideia de como fazer isso? 🤔

Primeiramente, precisamos descobrir a resistência equivalente do circuito. Temos que os resistores 2, 3 e 4 estão em paralelo, assim:

R 234 = 1 R 2 + 1 R 3 + 1 R 4 - 1 = R 2 R 3 R 4 R 2 R 4 + R 2 R 3 + R 3 R 4

Portanto a resistência equivalente é:

R e q = R 1 + R 2 R 3 R 4 R 2 R 4 + R 2 R 3 + R 3 R 4

Tranquilo até aqui? 👀

Passo 2

Temos que a fórmula da potência é:

P = ε 2 R e q

P = ε 2 R 1 + R 2 R 3 R 4 R 2 R 4 + R 2 R 3 + R 3 R 4 - 1

A partir dessa equação, vamos tentar isolar R 4 ...

R 1 + R 2 R 3 R 4 R 2 R 4 + R 2 R 3 + R 3 R 4 = ε 2 P

R 4 = ε 2 P - R 1 R 2 R 3 R 2 R 3 - ε 2 P - R 1 R 2 + R 3

Substituindo os valores do enunciado

R 4 = 24,0 2 60,0 - 7,00 12,0 4,00 12,0 4,00 - 24,0 2 60,0 - 7,00 12,0 + 4,00 - 1

R 4 = 19,5 Ω

Legal, né? 😉

Passo 3

(b) Como a potência depende do inverso da resistência o menor valor possível para R 4 é o valor que maximiza a potência, ou seja

R 4 = 0

(c) Usando o mesmo raciocínio do item (b), o valor que minimiza a potência é o maior valor para a resistência 4. Ou seja, que R 4 vá para infinito, fisicamente análogo a cortar o fio.

R 4 = ∞

Interessante... 😁

Passo 4

(d) Como R 4 é zero, toda a corrente passa por ele, assim a resistência equivalente só tem R 1 .

R e q = 7,0 Ω

Substituindo em P M a x

P m a x = 24,0 2 7,00 = 82,3 W

(e) Como o fio que liga a resistência 4 foi retirado, temos que:

R e q = R 1 + R 2 R 3 R 2 + R 3

Substituindo os valores do enunciado...

R e q = 7,0 + 12,0 4,00 12,0 + 4,00 = 10,0 Ω

Para essa resistência, temos

P m i n = 24,0 2 10 = 57,6 W

Entendeu tudo? Responde Aí!

Resposta

(a) R 4 = 19,5 Ω

(b) R 4 = 0

(c) R 4 = ∞

(d) P m a x = 82,3 W

(e) P m i n = 57,6 W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Fig. 27-77, as forças eletromotrizes das fontes ideais são ε 1 = 12,0 V e ε 2 = 4,00 V e as resistências são todas de 4,00 Ω . Determine (a) o valor absoluto de i_1; (b) o sentido (para cima ou par
Cada um dos três resistores indicados na Figura 26.62 possui uma resistência de 2,4Ω e pode consumir uma potencia máxima de 36 W sem se tornar excessivamente quente. Qual é a potencia máxima que o cir
No circuito indicado na Figura 26.64, um resistor de 20,0Ω está inserido em um grande bloco de gelo 0,0 ° C , e a bateria possui resistência interna desprezível. Qual é a taxa (em g/s) em que esse cir
62- Qual deve ser o valor da fem ϵ indicada na Figura 26.66 para que a corrente que passa no resistor de 7.0Ω seja igual a 1.80A ?Cada fonte de fem possui resistência interna desprezível.
64- ( a ) Calcule a corrente que passa em cada resistor e na bateria do circuito indicado na Figura 26.68 ( b ) Qual é a resistência equivalente do circuito?