Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 27.7 - Ex. 40

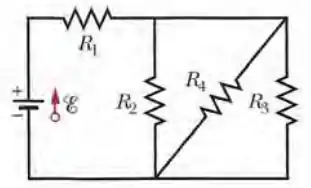
Na Fig. 27-53 , R 1 = 100 Ω , R 2 = R 3 = 50,0 Ω , R 4 = 75,0 Ω e a força eletromotriz da fonte ideal é E = 6,00 V . (a) Determine a resistência equivalente. Determine a corrente (b) na resistência 1; (c) na resistência 2; (d) na resistência 3; (e) na resistência 4.

Passo 1

Aqui temos um circuito com três resistores em paralelo R 2 , R 4 e R 3 logo temos que saber qual é a resistencia equivalente para depois somar com a ultima resistência em série com estas.

Passo 2

(a) Como os resistores R 2 , R 3 e R 4 estão em paralelo, a Eq. 27-24 nos dá uma resistência equivalente

R = R 2 R 3 R 4 R 2 R 3 + R 2 R 4 + R 3 R 4 = 50,0 Ω × 50,0 Ω × 75,0 Ω 50,0 Ω × 50,0 Ω + 50,0 Ω × 75,0 Ω + 50,0 Ω × 75,0 Ω = 18,8 Ω

Assim, considerando a contribuição do resistor R 1 , a resistência equivalente do circuito é R e q = R 1 + R = 100 Ω + 18,8 Ω = 118,8 Ω ≈ 119 Ω .

Passo 3

(b) i 1 = E R e q = 6,0 V 118,8 Ω = 5,05 × 10 - 2 A = 50,5 m A .

Passo 4

(c) i 2 = E - V 1 R 2 = E - i 1 R 1 R 2 = 6,0 V - 5,05 × 10 - 2 A × 100 Ω 50 Ω = 1,9 × 10 - 2 A

Passo 5

(d) i 3 = E - V 1 R 3 = i 2 R 2 R 3 = 1,9 × 10 - 2 A × 50 Ω 50 Ω = 1,9 × 10 - 2 A

Passo 6

(e) i 4 = i 1 – i 2 – i 3 = 5,05 × 10 - 2 A – 2 × 1,90 × 10 - 2 A = 1,25 × 10 - 2 A = 12,5 m A .

Resposta

(a) R e q ≈ 119 Ω .

(b) i 1 = 50,5 m A .

(c) i 2 = 1,9 × 10 - 2 A

(d) i 3 = 1,9 × 10 - 2 A

(e) i 4 = 12,5 m A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A Fig. 27-45 mostra uma parte de um circuito. As resistências são R 1 = 2,0 Ω , R 2 = 4,0 Ω e R 3 = 6,0 Ω e a corrente indicada é i = 6,0 A . A diferença de potencial entre os pontos A e B que ligam o
Duas fontes iguais de força eletromotriz ε = 12,0 V e resistencia interna r = 0,200 Ω podem ser ligadas a uma resistência R em paralelo (Fig. 27-52) ou em série (Fig. 27-53). Se R = 2,00 r , qual é a
Na Fig. 27-44, a corrente na resistência 6 é i 6 = 1,40 A e as resistências são R 1 = R 2 = R 3 = 2,00 Ω , R 4 = 16,0 Ω , R 5 = 8,00 Ω e R 6 = 4,00 Ω . Qual é a força eletromotriz da fonte ideal?
Na Fig. 27-46, ε = 12,0 V , R 1 = 2000 Ω , R 2 = 3000 Ω e R 3 = 4000 Ω . Determine as diferenças de potencial (a) V A - V B ; (b) V B - V C (c) V C - V D ; (d) V A - V C .
Na Fig. 27-54a, o resistor 3 é um resistor variável e a força eletromotriz da fonte ideal é E = 12 V . A Fig. 27-54b mostra a corrente i na fonte em função de R 3 . A escala horizontal é definida por