Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 27.7 - Ex. 44

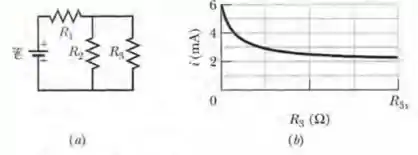
Na Fig. 27-54a, o resistor 3 é um resistor variável e a força eletromotriz da fonte ideal é E = 12 V . A Fig. 27-54b mostra a corrente i na fonte em função de R 3 . A escala horizontal é definida por R 3 S = 20 Ω . A curva tem uma assíntota de 2,0 m A para R 3 → ∞ . Determine (a) a resistência R 1 ; (b) a resistência R 2 .

Passo 1

Fala aí, pessoal!! 😊

Aqui temos um resistor variável em um circuito, temos no gráfico (b) a variação da corrente em função deste resistor.

Nosso objetivo é determinar a resistência R 1 e R 2 ...

Tem ideia de como fazer isso? 🤔

Para determinar R 1 , basta aplicarmos a lei de Ohm no circuito para R 3 = 0

V = R i

Já para determinar R 2 tambem podemos aplicar a lei de Ohm para R 3 = ∞

Veja só! 😉

Passo 2

(a) Quando R 3 = 0 , toda a corrente passa por R 1 e R 3 . Como o valor dessa corrente, de acordo com o gráfico da Fig. 27-55b, é 6   m A , a lei de Ohm nos dá

V = R 1 i → R 1 = V i

Se V = 12 V e i = 6 m A ...

R 1 = 12 V 6 · 10 - 3 A

R 1 = 2,0 · 10 3 Ω = 2,0 k Ω .

Tranquilo até aqui? 😁

Passo 3

(b) Quando R 3 = ∞ , toda a corrente passa por R 1 e R 2 . Como o valor dessa corrente, de acordo com o enunciado, é 2,0   m A , a lei de Ohm nos dá

V = R 1 + R 2 i

R 1 + R 2 = V i

R 2 = V i - R 1

Se V = 12 V , i = 2 m A e R 1 = 2 k Ω

R 2 = 12 2 · 10 - 3 - 2 · 10 3

R 2 = 4 · 10 3 Ω = 4 k Ω

E aí! Tudo certo? Responde Aí! 😉

Resposta

(a) R 1 = 2,0 k Ω

(b) R 2 = 4,0 k Ω

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quando duas resistências 1 e 2 são ligadas em série, a resistência equivalente é 16,0 Ω . Quando são ligadas em paralelo, a resistência equivalente é 3,0 Ω . Determine (a) a menor; (b) a maior das dua
Na Fig. 27-9, determine a diferença de potencial V d - V c entre os pontos d e c se ε 1 = 4,0 V , ε 2 = 1,0 V , R 1 = R 2 = 10 Ω , R 3 = 5,0 Ω e a fonte é ideal.
Na Fig. 27-42, as forças eletromotrizes das fontes ideais são E 1 = 5,0 V e E 2 = 12 V , as resistências são de 2,0 Ω e o potencial é tomado como zero no ponto do circuito ligado à terra. Determine os
A fonte ideal da Fig. 27-39a tem uma força eletromotriz E = 6,0 V . A curva I da Fig. 27-39b mostra a diferença de potencial V entre os terminais do resistor 1 em função da corrente i no resistor. A e
As duas fontes da Fig. 27-43a são ideais. A força eletromotriz E 1 da fonle 1 tem um valor fixo, mas a força eletromotriz E 2 da fonte 2 pode assumir qualquer valor entre 1,0 V e 10 V . Os gráficos da