Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 27.8 - Ex. 54

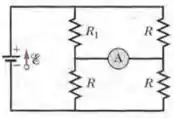
Na Fig. 27-60, R 1 = 2,00 R , a resistência do amperímetro é desprezível e a fonte é ideal. A corrente no amperímetro corresponde a que múltiplo de E / R ?

Passo 1

Fala aí! tudo certinho? 😉

Aqui temos um circuito que tem 4 resistores em paralelo e temos que saber a leitura do amperímetro (a corrente que passa por ele) em função de ℰ e R.

Parece complicado? 👀

A primeira coisa que podemos fazer é calcular a resistência equivalente do circuito e assim, pela lei de Ohm, calcular a corrente i na fonte...

Veja só! 👀

Passo 2

Como, de acordo com o enunciado, a resistência do amperímetro é desprezível, a queda de tensão no amperímetro é nula e, portanto, as correntes nos dois resistores de baixo têm o mesmo valor, que vamos chamar de i . Nesse caso, a corrente da fonte é 2 i . Como a resistência equivalente do circuito é

R e q = 2 R R 2 R + R + R R R + R = 7 6 R .

Logo

2 i = ε R e q

Portanto

i = ε 2 R e q

como R e q = 7 6 R

i = ε 2 7 6 R = 3 ε 7 R .

Tranquilo até aqui? 😊

Passo 3

Agora basta aplicar a lei das malhas na parte esquerda do circuito.

ε – i 2 R 2 R – i R = 0

Logo

i 2 R = ε – i R 2 R aqui o índice 2 R do i significa que a corrente que passa em uma resistência de 2 R

Fazendo

i = 3 ε 7 R

Obtemos

i 2 R = 2 ε 7 R .

Como a corrente no amperímetro é a diferença entre i 2 R e i , temos: pois é a corrente total menos a corrente que passa em R 1

i a m p = i - i 2 R = 3 ε 7 R - 2 ε 7 R = ε 7 R

Então

i a m p ε / R = 0,143

Legal, né? O que achou? Responde Aí! 😉

Resposta

i a m p ε / R = 0,143

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Você recebe um galvanômetro D'Arsonval que desviará da escala completa se uma corrente de 50,0 μ A passar pelo galvanômetro. Nesta corrente, há uma queda de tensão de 0,250 V no medidor. Você deseja u
Prove que, quando a chave S na Fig. 29-15 é movida de a para b, toda a energia armazenada no capacitor é transformada em energia térmica no resistor. Suponha que o capacitor esteja totalmente carregad
Qual é a corrente, em termos de E e R, indicada pelo amperímetro da Fig. 29-41? Suponha que a resistência do amperímetro seja nula e que a bateria seja ideal.
Quantas constantes de tempo devem decorrer até que um capacitor em um circuito RC em série esteja carregado com menos de 1,0% de sua carga de equilíbrio?
(Veja o Problema 60). Para medir uma resistência, os medidores podem também ser ligados como mostra a Fig. 29-43b. Novamente, a razão das leituras dos medidores dá apenas um valor aparente R‘ para a r