Na fig 35-39 duas fontes pontuais isotrópicas, , estão no eixo , separadas por uma distância de , e emitem em fase com um comprimento de onda de . Um detector de luz é colocado no ponto , situado no eixo , a uma distância da origem. Qual é o maior valor de , para o qual a luz detectada é mínima devido a uma interferência destrutiva?

Agora vamos olhar com carinho o desenho para conseguir determinar esses percursos:

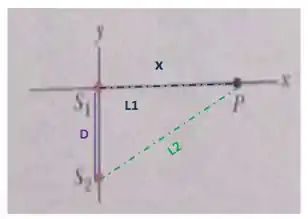
O percurso percorrido pela onda até o detector é , mas o caminho percorrido pela segunda onda é aquele ali. Mas como podemos encontrar esse caminho em termos dos valores que temos? Ah! PITÁGORAS!!

A hipotenusa é nosso caminho e os catetos são e como desenhei ali em cima, daí o caminho é:

E assim podemos substituir na condição para interferência destrutiva:

Para termos o maior valor de , precisamos que o valor de seja mínimo, então :

Agora vou fazer algumas manipulações matemáticas para tentar isolar esse aí:

Agora elevando os dois lados ao quadrado:

E abrindo o produto notável:

Cortando dos dois lados

E como temos que ( e ), então nossa conta fica bem simplificada, saca só:

E temos o valor do comprimento de onda! Agora sim conseguimos encontrar :