Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 37.3 - Ex. 26
Na fig 37-9 o observador S observa dois clarões. Um grande clarão acontece em e, pouco tempo depois, um pequeno clarão acontece em O intervalo de tempo é . Qual é o menor valor de para o qual os dois clarões podem ocorrem na mesma coordenada x’ para o observador S’ ?
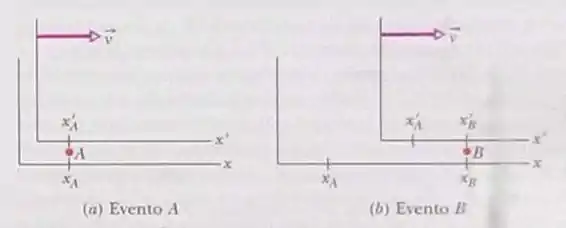
Passo 1
Temos coordenadas no e no :
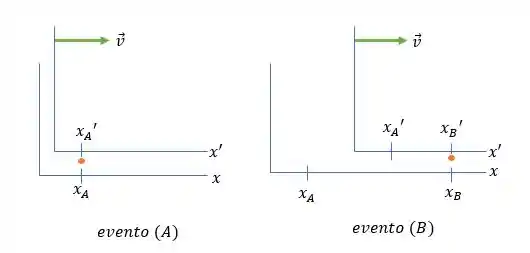
Estamos interessados em calcular o valor de para que
No caso limite onde , ou seja, onde o modulo da velocidade se aproxima da velocidade da luz, assim temos:
Resposta
O menor valor de é de .
Exercícios de Livros Relacionados
Para os sistemas de coordenadas da fig 37-25, os eventos A e B ocorrem nas seguintes coordenas espaçotemporais: no referencial S, ( x A , t A ) e ( x B , t B ) ; no referencial S’, ( x ' A , t ' A ) e
Inversão relativística da ordem de dois eventos. As figs 37-25ª e 37-25b mostram uma situação (usual) em que um referencial S’passa por um referencial S, na direção positiva comum dos eixos x e x’, mo
O observador S’ passa pelo observador S movendo-se ao longo da direção comum dos eixos x’e x, e levando três réguas de 1 metro: a régua 1, paralela ao eixo x’, a régua 2, paralela ao eixo y’ e a régua
Na fig 37-9 o observador S detecta dois clarões. Um grande clarão acontece em x 1 = 1200 m e 5 μ s mais tarde, um pequeno clarão acontece em x = 480 m . De acordo com o observador S’, os dois clarões