Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 4- Ed: 10º - Capítulo 37.3 - Ex. 22

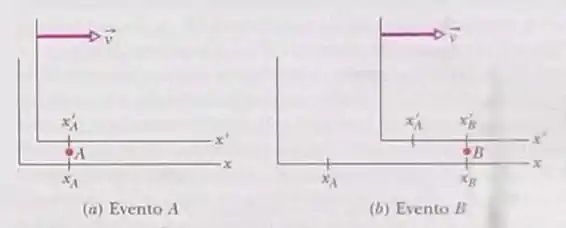
Para os sistemas de coordenadas da fig 37-25, os eventos A e B ocorrem nas seguintes coordenas espaçotemporais: no referencial S, ( x A , t A ) e ( x B , t B ) ; no referencial S’, ( x ' A , t ' A ) e ( x ' B , t ' B ) . No referencial S, Δ t = t B - t A = 1 μ s e Δ x = x B - x A = 400 m . (a) Escreva uma expressão para Δ x ' em termos do parâmetro de velocidade e dos dados do problema. Faça um gráfico de Δ x ' em função de β para duas faixas de valores: (b) 0 ≤   β ≤ 0,01 e (c) 0,1 ≤   β ≤ 1 . (d) Para que valor de β a distância espacial Δ x ' é mínima? (e) Qual é o valor da distancia mínima?

Passo 1

(a) Temos que a diferença de coordenadas é

Δ x ' = γ Δ x - v Δ t = γ Δ x - β c Δ t = γ 400 - β c 1 ⋅ 10 - 6 = 400 - 299,8 β 1 - β 2  

Passo 2

(b) Utilizando a expressão encontrada no passo 1, podemos plotar o seguinte gráfico para o intervalo desejado:

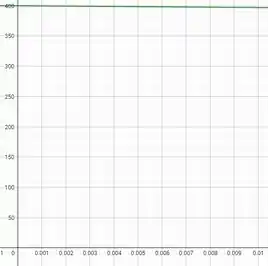
Passo 3

(c) Para esse novo intervalo, temos o seguinte gráfico:

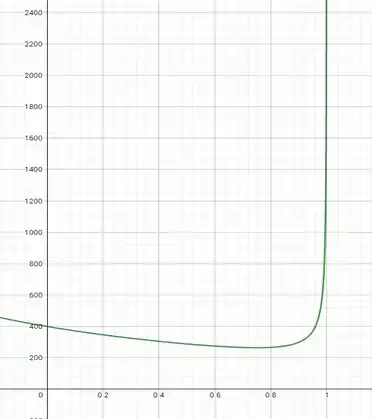
Passo 4

(d) Para determinar o valor de β para o qual a distancia espacial é mínima, fazemos a seguinte derivada e a igualamos a 0:

d Δ x ' d β = d d β Δ x - β c Δ t 1 - β 2 = β Δ x - c Δ t 1 - β 3 / 2   = 0

O numerador deve ser nulo, logo, isolando o coeficiente de velocidades temos:

β = c Δ t Δ x = 2,998 ⋅ 10 8 ⋅ 1 ⋅ 10 - 6 400 = 0,7495 ≈ 0,750

Passo 5

(e) Substituindo o valor de β calculado no passo 4 na expressão do passo 1, temos:

Δ x ' = 264,8 m ≈ 265 m

Resposta

(d) O valor de beta procurado é 0,750.

(e) A distancia mínima é de 265m.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A Fig. 37-16 mostra uma nave (cujo referencial é S ' ) passando por um observador (cujo referencial é S ) com velocidade v → = 0.950 ⋅ c ⋅ i → . Um próton é emitido com uma velocidade de 0,980 ⋅c ao l
O referencial S ' passa pelo referencial S com uma certa velocidade, como na Fig. 37-9. Os eventos 1 e 2 estão separados por uma distância Δ x ' de acordo com um observador em repouso no referencial S
Distancia temporal entre dois eventos. Os eventos A e B ocorrem nas seguintes coordenadas espaçotemporais nos referenciais da Fig. 37-25: no referencia S , ( x a , t a ) e ( x b , t b ) ; no referenci
Distancia temporal entre dois eventos. Os eventos A e B ocorrem nas seguintes coordenadas espaçotemporais nos referenciais da Fig. 37-25: no referencia S , ( x a , t a ) e ( x b , t b ) ; no referenci
O problema do carro na garagem. Mário acaba de comprar a maior limusine do mundo, com um comprimento próprio L=30,5m . Na Fig. 37-32a, o carro aparece parado em frente a uma garagem cujo comprimento p