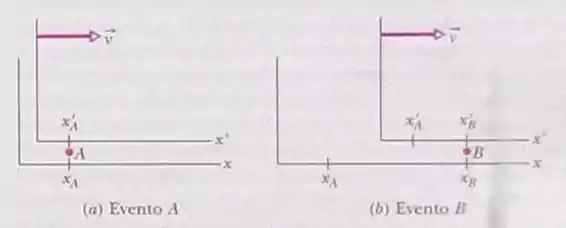
Inversão relativística da ordem de dois eventos. As figs 37-25ª e 37-25b mostram uma situação (usual) em que um referencial S’passa por um referencial S, na direção positiva comum dos eixos x e x’, movendo-se com velocidade constante v em relação a S. O observador 1 está em repouso no referencial S e o observador 2 está em repouso no referencial S’. As figuras também mostram eventos A e B que ocorrem nas seguintes coordenadas do espaço-tempo, expressas nos dois referenciais:
Evento Referencial S Referencial S’
A
B
No referencial S, o evento A ocorre antes do evento B, com uma distância temporal e uma distância espacial . Seja a distância temporal dos eventos de acordo com o observador 2. (a) Escreva uma expressão para em termos do parâmetro de velocidade e dos dados do problema. Faça um gráfico de em função de para os seguintes intervalos: (b) (baixas velocidades, ) e (c) (altas velocidades, ). (d) Para que valor de a distância temporal é nula? Para que faixa de valores de a sequencia dos eventos A e B para o observador 2 é (e) a mesma que para o observador 1 e (f) não é a mesma que para o observador 1? (g) O evento A pode ser a causa do evento B ou vice-versa? Justifique sua resposta.
Passo 1
A transformação de Lorentz para os espacos é
A transformação de Lorentz para os tempos é
Passo 2
(a) Temos que
Passo 3
(b) Para o intervalo dado, temos que o gráfico de é
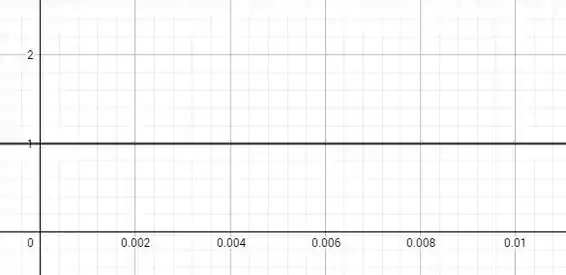
O gráfico não pode ser distinguido de uma reta horizontal. Isso ocorre porque, para valores pequenos do parâmetro de velocidade, a distancia temporal entre os eventos medida pelo observador 2 é praticamente igual à distancia medida pelo observador 1. Em outras palavras, neste caso não são observador os efeitos relativísticos.
Passo 4
(c) Para o intervalo dado, temos que o gráfico de é
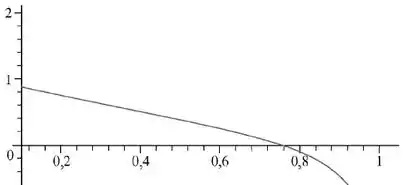
Passo 5
(d) Fazendo
Temos:
Passo 6
(e) De acordo com o passo 4, a sequencia dos eventos para o observador 2 é a mesma que para o observador 1 para , pois .
Passo 7
(f) De acordo com o passo 4, a sequencia dos eventos para o observador 2 é a mesma que para o observador 1 para , pois .
(g) Não, o evento A não pode ser a causa do evento B, pois um sinal não pode se propagar com uma velocidade maior do que a da luz.
Resposta
(d) O parâmetro de velocidade é.
(e) A sequencia dos eventos é a mesma.
(f) A sequencia dos eventos não é a mesma.
(g) O evento A não pode ser a causa do evento B.