Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 37.3 - Ex. 25
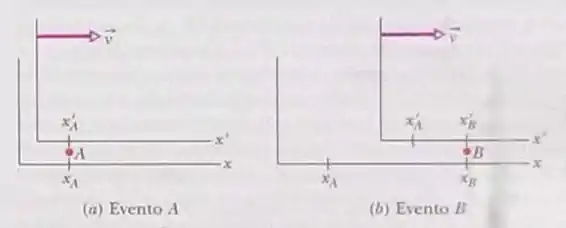
Na fig 37-9 o observador S detecta dois clarões. Um grande clarão acontece em e mais tarde, um pequeno clarão acontece em . De acordo com o observador S’, os dois clarões acontecem na mesma coordenada x’. (a) Qual é o parâmetro de velocidade de S’? (b) S’ está se movendo no sentido positivo ou negativo do eixo x? De acordo com S’, (c) qual dos dois clarões acontece primeiro? (d) Qual é o intervalo de tempo entre os dois clarões?
Passo 1
(a) No referencial S, as coordenadas são tais que para o grande e para o pequeno clarão.
Assim:
Fazendo na transformação de Lorentz temos:
O que nos resulta
Consequentemente o fator de velocidade é
Passo 2
(b) O sinal negativo obtido no passo 1 nos mostra que o referencial S’ está se movebdo no sentido negativo do eixo x.
Passo 3
(c) De acordo com a transformação de Lorentz:
Para qualquer valor de gama, essa expressão retorna um valor positivo. Dessa forma, a ordem dos clarões no referencial S’ é a mesma que no referencial S. O grande clarão ocorre antes.
Passo 4
(d) Terminando o calculo iniciado no passo 3, temos:
Resposta
(a) O parâmetro de velocidade é .
(b) O referencial S’se move no sentido negativo de x.
(c) O grande clarão ocorre primeiro.
(d) O intervalo de tempo é de .