Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 37.3 - Ex. 17
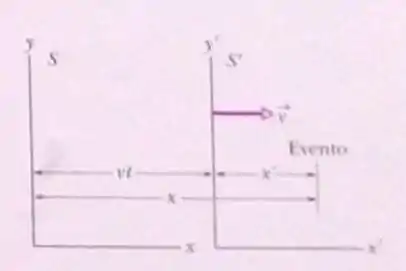
Na fig 37-9, as origens dos dois referenciais coincidem em t=t’=0 e a velocidade relativa é 0,950c. Dois micrometeoritos colodem nas coordenadas x=100 km e t=200s de acordo com um observador estacionário no referencial S. Determine as coordenadas (a) espacial e (b) temporal da colisão de acordo com um observador no referencial S’.
Passo 1
A transformação de Lorentz para os espacos é
A transformação de Lorentz para os tempos é
Passo 2
(a) Utilizando a transformação de Lorentz descrita no passo 1, temos:
Onde,
O que nos dá
Passo 3
(b) De acordo com a segunda equação do passo 1, temos que
Resposta
(a) A coordenada espacial é de .
(b) A coordenada temporal é de .
Exercícios de Livros Relacionados
Uma longa haste paralela ao eixo x é liberada do repouso. Subsequentemente, ele está em queda livre com uma aceleração de magnitude g na direção –y. Um observador em um foguete se movendo com velocida
A equação para a frente de onda esférica de um pulso de luz que começa na origem no tempo t = 0 é x2 + y2 + z2 - (ct) 2 = 0. O quadro S ′ se move com velocidade v ao longo do eixo x. Usando a transfor
Um astronauta que se exercita em uma esteira está com uma pulsação de 150 por minuto. Se ele caminha por 1,00 h, de acordo com o relógio de bordo, a uma velocidade de 1,00 m/s, enquanto a nave viaja a
Um trem relativístico com 200 m de comprimento próprio se aproxima de um túnel com o mesmo comprimento próprio, a uma velocidade relativa de 0,900c. Uma bomba de tinta na locomotiva está programada pa
A Fig. 37-37 mostra três situações nas quais uma espaçonave passa pela Terra (representada por um ponto) e, em seguida, faz uma viagem de ida e volta à Terra, com o fator de Lorentz indicado. As distâ