Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 4.6 - Ex. 55
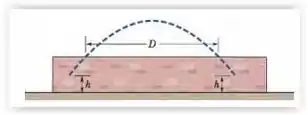
Na Fig. 4-44, uma bola de beisebol é golpeada a uma altura e apanhada na mesma altura. Deslocando-se paralelamente a um muro, passa pelo alto do muro após ter sido golpeada e, novamente, depois, quando está descendo, em posições separadas por uma distância . (a) Qual é a distância horizontal percorrida pela bola do instante em que foi golpeada até ser apanhada? Quais são (b) o módulo e (c) o ângulo (em relação à horizontal) da velocidade da bola imediatamente após ter sido golpeada? (d) Qual é a altura do muro?
Passo 1
Bom pessoal , sejam as coordenadas do ponto no qual a bola é golpeada. Sejam e (altura do muro) as coordenadas do ponto no qual a bola passa pela primeira vez pelo ponto mais alto do muro, após ter sido golpeada, e sejam e as coordenadas do ponto no qual a bola passa novamente pelo ponto mais alto do muro, depois. Sejam e as cooordenadas do ponto no qual a bola é apanhada. As distâncias estão em metros e os tempos em segundos.
Lembrando que é constante, temos , o que nos dá . Assim, após seis segundos, temos:
Passo 2
Agora nós podemos aplicar a equação à componente vertical do movimento da bola no trecho em que está acima do ponto mais alto do muro, dessa forma , obtemos:
Da qual . Um segundo antes, usando a equação , obtemos . Assim, a velocidade inicial da bola é :
Podemos achar o módulo da velocidade através da fórmula :
Até aqui tranquilo ? Bora continuar que ainda não acabou!
Passo 3
Podemos achar o ângulo em relação á horizontal da forma como já conhecemos :
Podemos interpretar esse resultado como uma velocidade de e ângulo apontado pra direita e pra cima .
Passo 4
Durante o primeiro do movimento a trajetória vertical da bola é dada por e, portanto,
Tranquilo galera???? Bora resolver mais questões então!!!!!!
Resposta
Ei, a resposta está no passo a passo :)