Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 4.Problemas Adicionais - Ex. 87

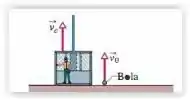
Na Fig. 4-55, uma bola é lançada verticalmente para cima, a partir do solo, com uma velocidade inicial v 0   =   7,00   m / s . Ao mesmo tempo, um elevador de serviço começa a subir, a partir do solo, com uma velocidade constante v c =   3,00   m / s . Qual é a altura máxima atingida pela bola (a) em relação ao solo e (b) em relação ao piso do elevador? Qual é a taxa de variação da velocidade da bola (c) em relação ao solo e (d) em relação ao piso do elevador?

Passo 1

Então galera , como o movimento é uniformemente variado , sabemos que

v 2 = v 0 2 - 2 g h

Logo:

h = v 0 2 - v 2 2 g

Como v = 0 na altura máxima e v 0 = 7,00   m/s , temos que:

h = 7,00   m/s 2 - 0 2 9,8   m/s²

h = 2,5   m

Passo 2

A velocidade relativa pode ser calculada como de costume através da fórmula

v r = v 0 - v c

Logo:

v r = 7,00   m/s - 3 , 00   m/s

v r = 4 , 00   m/s

Isso em relação ao piso do elevador, beleza? Usando a equação para a altura, obtemos:

h = 4,00   m/s 2 - 0 2 2 9,8   m/s²

h = 0,82   m

Passo 3

Iradoso, agora na letra (c), a aceleração da bola é conhecida desde o começo, já que taxa de variação da velocidade da bola em relação ao solo é a própria aceleração da gravidade:

a = 9,80   m/ s 2

Passo 4

Como o elevador está se movendo com velocidade constante, a taxa de variação da velocidade da bola em relação ao elevador também deve ser 9,80   m/ s 2 , beleza pessoal?

Resposta

  1. h = 2,5   m
  2. h = 0,82   m
  3. a = 9,80   m/ s 2
  4. a = 9,80   m/ s 2

Tranquilo galera ? Bora resolver mais exercícios então

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

(a) Com que velocidade deve ser lançada uma bola verticalmente a partir do solo para que atinja uma altura máxima de 50 m? (b) Por quanto tempo permanece no ar? (c) Esboce os gráficos de y , v e a em
Uma chave cai verticalmente de urna ponte que está 45 m acima da água. A chave atinge um barco de brinquedo que está se movendo com velocidade constante e se encontrava a 12 m do ponto de impacto quan
Um tatu assustado pula verticalmente para cima, subindo 0,544m nos primeiros 0,200s . (a) Qual é a velocidade do animal ao deixar o solo? (b) Qual é a velocidade na altura de 0,544m ? (c) Qual é a alt
Um parafuso se desprende de uma ponte em construção e cai 90 m até chegar ao solo. (a) Em quanto tempo o parafuso percorre os últimos 20% da queda? Qual é a velocidade (b) quando começam os últimos 20
Uma pedra é deixada cair em um rio a partir de uma ponte situada 43,9m acima da água. Outra pedra é atirada verticalmente para baixo 1,0s após a primeira ter sido deixada cair. As pedras atingem a águ