Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 2.9 - Ex. 47
(a) Com que velocidade deve ser lançada uma bola verticalmente a partir do solo para que atinja uma altura máxima de 50 m? (b) Por quanto tempo permanece no ar? (c) Esboce os gráficos de , e em função de para a bola. Nos dois primeiros gráficos, indique o instante no qual a bola atinge a altura de 50 m.
Passo 1
(a) Galera, quando a altura é máxima, a velocidade será zero!! Isso porque é o ponto onde o objeto para de subir e começa a cair. Ok?
Sabendo disso, vamos pôr as informações que temos na equação de Torricelli dada como:
Isolando :
Como a velocidade final é nula, , dado e , vamos obter que:
Passo 2
(b) Vamos usar a função horária da velocidade para descobrir o tempo de subida da bola:
Isolando :
A bola sobe e desce, certo? E como o tempo de subida é igual ao de descida, então ela permanece no ar um tempo igual duas vezes seu tempo de subida. Portanto, ela fica no ar por .
Passo 3
(c) Pela função horária da posição:
Sabemos que a velocidade é a derivada da função posição e que a aceleração é a derivada da velocidade, então temos:
Plotando essas funções, vamos obter que:
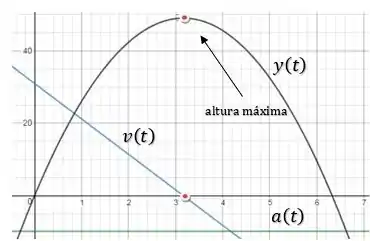
A indicação de quando a bola atinge os 50m de altura está nessas bolinhas vermelhas.
Prontinho! 😊
Resposta
a)
b)
(c) 