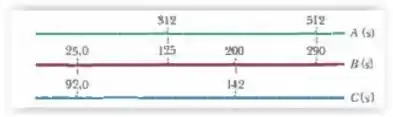
Três relógios digitais, A, B e C, funcionam com velocidades diferentes e não têm leituras simultâneas de zero. A Fig. 1-6 mostra leituras simultâneas de pares dos relógios em quatro ocasiões. (Na primeira ocasião, por exemplo, B indica 25,0 s e C indica 92,0 s) .Se o intervalo entre dois eventos é 600 s de acordo com o relógio A, qual é o intervalo entre os eventos :
(a) no relógio B ?
(b) no relógio C?
(c) Quando o relógio A indica 400 s, qual é a indicação do relógio B?
(d) Quando o relógio C indica 15,0 s, qual é a indicação do relógio B?
(Suponha que as leituras sejam negativas para instantes anteriores a zero).
Passo 1
Vamos lá!! Nesse tipo de exercício o que devemos fazer é buscar uma relação entre os componentes (neste caso , os relógios) e para isso é fundamental retirar as informações úteis presentes em textos e figuras . Neste caso , por exemplo , a figura apresenta o comportamento dos relógios com o passar do tempo e é a partir daí que vamos estruturar nosso problema.
- Em um dado evento, o relógio A indicou uma variação de 600s, quantos segundos o relógio B indicaria?
- Nessa segunda questão precisamos achar a relação de e utilizando o relógio , pois a imagem não traz uma indicação de proporção entre o primeiro e o terceiro relógio.
- Vamos contiiinuaar!
- Essa vai ser beem parecida com a questão anterior, só que vamos usar a relação dos relógios e :
Bom, sabemos que há uma relação entre a variação de tempo do relógio A e do relógio B, o que iremos fazer aqui é uma regra de três:
Os valores que coloquei no denominador da nossa fração, é a variação de tempo marcado por cada relógio entre as ocasiões 2 e 4, que são ocasiões que temos a marcação dos relógios A e B.
Agora, para encontrar a variação em B, é só substituir o nosso por 600s.
Assim, resolvendo a continha
Beleza?!
Passo 2
Assim, a razão de por é
Agora, como sabemos que a variação em A de 600s, equivale a uma variação em B de 495s, podemos encontrar nossa variação em C!
Show de bola?!
Passo 3
Agora, não queremos mais encontrar a leitura para uma variação de tempo, mas sim a leitura de um relógio para um determinado instante.
No caso, temos que a leitura no relógio A é de 400s, então qual seria a leitura no relógio B?
Olhando para a nossa escala, nós temos:
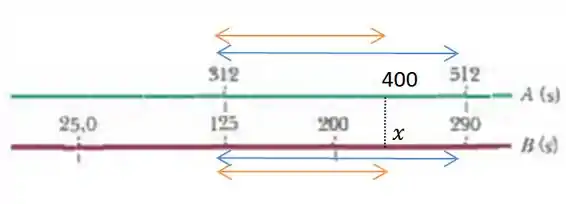
Nossa regra de três vai consistir da proporção dada pelas setas que coloquei na escala...
Agora é só fazer a continha para encontrar o valor de .
Beleza?!
Passo 4
Olhando para a nossa escala:
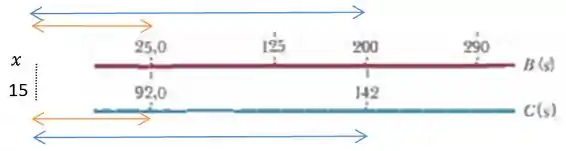
A regra de três vai ficar...
Agora é encontrar o x e partir pro abraço!