Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 6.Problemas Adicionais - Ex. 95

Durante a tarde, um carro é estacionado em uma ladeira que faz um ângulo de 35,0 ° com a horizontal. Nesse momento, o coeficiente de atrito estático entre os pneus e o asfalto é 0,725 . Quando anoitece, começa a nevar e o coeficiente de atrito diminui, tanto por causa da neve como por causa das mudanças químicas do pavimento causadas pela queda de temperatura. Qual deve ser a redução percentual do coeficiente de atrito para que o carro comece a escorregar ladeira abaixo?

Passo 1

Olá, querido! Tudo bem?

Você pode pensar que esse carro na ladeira é analago a um bloco sobre uma rampa. A rampa é a ladeira, então ela tem uma inclinação de θ = 35 ° .

Aí a gente tem algo assim:

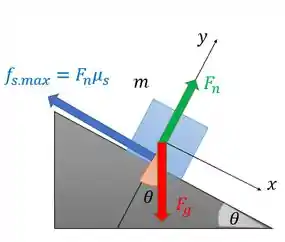
Então, esse carro pode deslizar pela ladeira quando o coeficiente de atrito muda quando anoitece. Ou seja, a partir da nossa interpretação, o bloco pode deslizar pela rampa se μ s for pequeno o suficiente. Aí o que precisamos fazer é achar o coeficiente μ s que permite isso.

Por que? Porque aí a gente compara ele com o coeficiente de 0,725 como ele pede.

A situação limite de deslizamento é quando a força de atrito estático é máxima, e vale f s . m á x   = μ s F n . Então essa situação limite vai nos dar o mínimo valor de μ s que precisamos.

Bora usar a segunda lei de Newton e descobrir o valor desse cara!

Passo 2

De acordo com a 2° Lei de Newton no eixo x para o carro, vamos ter

∑ F x = m a x

Como estamos em equilíbrio, a x = 0 , então:

∑ F x = 0

Aí nessa direção, a gente temos f s . m á x = F n μ s , no sentido negativo se opondo a tendência de movimento. E temos também a componente x de F g que é dada por F g x = m g s e n θ que aponta para x positivo.

O somatório de forças fica

- F n μ s   + m g s e n θ = 0

F n μ s = m g s e n θ     i

Passo 3

Agora a segunda lei de Newton para a direção y , sabendo que a y = 0 :

∑ F y = m a y → ∑ F y = 0

Nessa direção temos a força normal para a parte positiva e a componente y de F g para baixo. O somatório fica:

F n - m g c o s θ = 0

F n = m g c o s θ   i i

Passo 4

Dividindo a equação i pela i i :

F n μ s F n = m g s e n θ m g c o s θ

μ s = tan ⁡ ( θ )

Como θ = 3 5 ° :

μ s = tan ⁡ 3 5 °

μ s = 0,700

Passo 5

Para a gente achar o percentual que isso representa de 0,725 , fazemos:

μ s 0,725 × 100 = 0,7 0,725 × 100 = 96,6 %

Então o percentual de redução que a gente tem quando sai de 0,725 para 0,7 é

100 % - 96,6 % = 3,4 %

Resposta

A redução deve ser de 3,4 % do coeficiente de atrito.

De boa galera??? Bora resolver mais questões então

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

a) Se o coeficiente de atrito cinético entre os pneus e um pavimento seco for de 0,80 , qual é a menor distância para fazer um carro parar bloqueando o freio, quando o carro se desloca a 28,7m / s ? b
Considere o sistema indicado na Figura 5.54 . O bloco A pesa 45N e o bloco B , 25N . Suponha que o bloco B desça com velocidade constante. a) Ache o coeficiente de atrito cinético entre o bloco A e o
Um carregador de supermercado empurra uma caixa com massa de 11,2k g sobre uma superfície horizontal com uma velocidade constante de 3,50m / s . O coeficiente de atrito cinético entre a caixa e a supe
Você está baixando duas caixas por uma rampa, uma sobre a outra, e como indica a Figura 5.53 você faz isso puxando uma corda paralela à superfície da rampa. As duas caixas se movemjuntas, a uma veloci
Você verifica que é necessária uma força de 160N para deslizar uma caixa ao longo da superfície de um piso plano, a uma velocidade escalar constante. O coeficiente de atrito estático é 0,52 e o coefic