Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.3 - Ex. 33
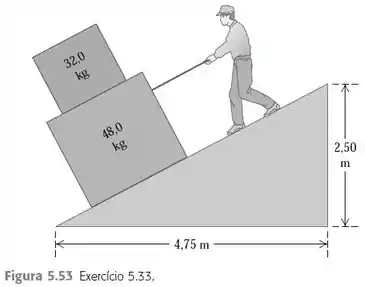
Você está baixando duas caixas por uma rampa, uma sobre a outra, e como indica a Figura 5.53 você faz isso puxando uma corda paralela à superfície da rampa. As duas caixas se movem
juntas, a uma velocidade escalar constante de 15,0 cm/s. O coeficiente do atrito cinético entre a rampa e a caixa inferior é 0,444, e o coeficiente de atrito estático entre as duas caixas é 0,800. a) Qual força você deve aplicar para realizar isso? b) Qual o módulo, a direção e o sentido da força de atrito sobre a caixa superior?
Passo 1
Primeiro passo é fazer um diagrama de corpo livre para cada uma das caixas, vamos representa-la na própria figura 5.53 para facilitar nossa visualização:
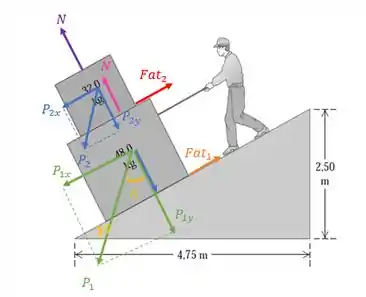
O bloco descerá com uma velocidade constante, isso significa que a força resultante nos dois blocos é nula, ou seja, as forças que puxam os blocos para a direita são iguais às forças que os puxam para a esquerda. Dessa forma, podemos equacionar da seguinte forma:
Pela 3º Lei de Newton, a , que é aplicada no bloco 2 (direcionada para a direita) gera uma reação no bloco 1, de mesmo módulo, mas com sentindo contrário. Essa força de atrito, corresponde a:
Passo 2
Agora, precisamos decompor os pesos de acordo com o eixo e :
Sendo o ângulo entre a horizontal e o plano inclinado, temos que:
Analisando o triângulo retângulo do plano inclinado, podemos inferir que:
Então:
Passo 3
Além disso, vamos definir a força de atrito, sabemos que:
Logo,
Com todas as informações que juntamos, podemos voltar a equação 1. Então temos que:
A normal , que age no bloco 1, pelo fato de o bloco estar se movimentando apenas no plano inclinado, é igual a soma de e . Desta forma:
Passo 4
O que temos que fazer agora é substituir a equação 4 na equação 3. Assim, ficamos com:
Isolando :
Colocando em evidencia:
Passo 5
Vamos aplicar a 1º Lei de Newton, , na caixa de cima, temos que:
Com direção para cima, na rampa.