Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 22.4 - Ex. 6
Duas partículas são mantidas fixas no eixo : a partícula 1, de carga , no ponto , e a partícula 2, de carga , no ponto . Qual é o campo elétrico total a meio caminho entre as partículas, em termos dos vetores unitários?
Passo 1
E aí! tudo certinho? 🤔
Bem, o enunciado nos fala que há duas partículas que estão no eixo x, e ele quer saber qual o campo elétrico exatamente no meio do caminho entre essas partículas. Primeiro, nós temos que calcular qual o meio do caminho entre as duas partículas, que é
Para calcular o campo elétrico entre as duas partículas, utilizaremos a fórmula de campo elétrico produzido por uma carga pontual:
Em que é a distância do ponto em que se está calculando o campo até a partícula, é a carga total. O termo , em que é a constante eletrostática
Bora lá! 😉
Passo 2
Agora que sabemos as distâncias e as cargas, podemos calcular o campo elétrico devido a cada partícula e somar os dois! Mas eu falei apenas do módulo, e quanto ao vetor? Bem, como o ponto que queremos calcular é no eixo x também, assim como as cargas, é natural que o vetor seja no mesmo sentido do eixo x. Utilizando a notação e , o campo elétrico será naturalmente na direção do vetor .
Agora devemos olhar o sentido do campo elétrico de cada partícula antes de fazer os cálculos para não nos confundirmos. Chamaremos de o campo elétrico devido a partícula 1. Como o ponto que nós estamos calculando o campo está depois do ponto da partícula 1 e a carga dela é negativa, então o campo devido a ela tem sentido decrescente (, olhe a figura abaixo.
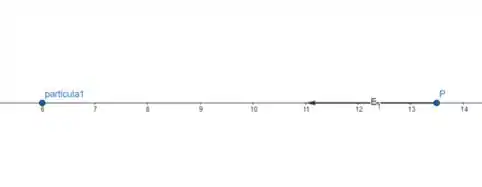
Chamaremos o campo devido a partícula 2 de , como o ponto está à esquerda da partícula 2 e a carga dela é positiva, então o campo tem o sentido decrescente também (, olhe a figura abaixo:
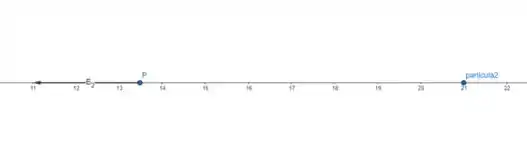
Agora que nós sabemos os sentidos dos campos basta apenas que a gente calcule o módulo, pois já sabemos os sentidos 😊.
Veja só! 😬
Passo 3
Usando a fórmula que nós relembramos no passo 1 para cálculo do campo, podemos calcular o campo devido as duas partículas:
Como os dois campos são no sentido decrescente do eixo :
Assim, basta somar os campos para conseguir o campo total:
E aí! o que achou? Responde Aí! 👀
