Fig. 21-38, duas pequenas esferas condutoras de mesma massa e mesma carga estão penduradas em fios não condutores de comprimento . Suponha que o ângulo é tão pequeno que a aproximaçâo pode ser usada. (a) Mostre que a distância de equilíbrio entre as esferas é dada por

E aí galerinha, vamos destruir essa questão comigo? Vamos láaaa!

(a) A figura a seguir mostra o diagrama de corpo livre da esfera da esquerda. A força da gravidade aponta para baixo, a força eletrostática da outra esfera aponta para a esquerda e a tensão do fio aponta na direção do fio, que faz um ângulo com a vertical. Como a esfera está em equilíbrio, a aceleração é zero. A componente da segunda lei de Newton nos dá e a componente dá . De acordo com a primeira equação, . Substituindo esse resultado na segunda equação, obtemos .

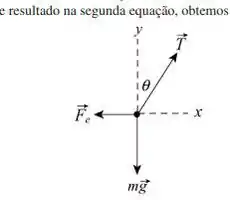
Aplicando relações trigonométricas ao triângulo da Fig. 21-38 formado pelo ponto de suspensão e as duas esferas, obtemos:

Se é muito maior que (o que acontece se for muito pequeno), podemos desprezar o termo do denominador e fazer . De acordo com a Eq. 21-1, o módulo da força eletrostática que uma das esferas exerce sobre outra é