Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 2.1 - Ex. 51
A figura 2-39 mostra a posição de uma partícula como função do tempo. Ache as velocidades médias para os intervalos de tempo a, b, c e d indicados na figura.
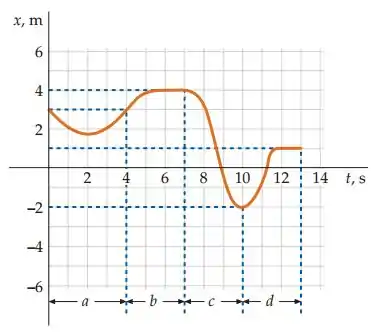
Figura 2-39
Passo 1
Olá, querido! A gente tem um gráfico velocidade posição versus tempo, onde o tempo é a variável do eixo horizontal e a posição é a variável do eixo vertical. E ele pede a velocidade no intervalo , , e , ou seja, ele pede , , e .
A expressão da velocidade média é dada por
Sendo o deslocamente e o tempo decorrido. Vamos ter que achar essas informações pelo gráfico.
O deslocamento é a variação de posição
Ou seja, para achar o deslocamento em cada caso, a gente vai precisa fazer a coordenada vertical do ponto final do intervalo, menos a a coordenada vertical do ponto inicial do intervalo. Então vamos calcular uma variação vertical no nosso gráfico.
Já o o tempo decorrido é variação de tempo:
Ele é a diferença entre a coordenada horizontal do ponto final menos a coordenada horizontal do ponto inicial. Como o tempo final é sempre maior (porque o tempo sempre aumenta), na real, vai ser a largura do intervalo que vamos avaliar, ok?
Agora é partir para as cotinhas!
Passo 2
()
Note que é marcado um número múltiplo de 2 a cada 2 quadrados, portanto cada quadrado de marcação corresponde a uma unidade.
Assim, para o intervalo , vamos ter que o ponto inicial está em
Desse modo, temos que
Já para o ponto final
Substituindo esses dados na expressão da velocidade média:
Passo 3
() Vamos fazer a mesma coisa aqui, mas agora para o intervalo
Vamos ter que o ponto inicial está em
Desse modo, temos que
Já para o ponto final
Substituindo esses dados na expressão da velocidade média:
Passo 4
() Fazendo a mesma coisa para o intervalo , achamos essas coordenadas:
Substituindo na expressão da velocidade média:
Passo 5
() Agora para o intervalo :
Substituindo