Um bloco de massa está sobre uma mesa horizontal (figura abaixo). O bloco é puxado por uma corda sem massa com uma força a um ângulo . O coeficiente de atrito estático é 0,60. O valor mínimo da força necessária para mover o bloco depende do ângulo . (a) Discuta qualitativamente como você espera que a magnitude desta força dependa de . (b) Calcule a força para os ângulos = 0º, 10º, 20º, 30º, 40º, 50º e 60º, e faça um gráfico de versus para mg = 400 N. De seu gráfico, para qual ângulo é mais eficiente aplicar a força para movimentar o bloco?

Letra (b)

Vamos começar aplicando a segunda lei de Newton:

Só que a gente vai considerar que a força de atrito estático é máxima, ou seja, o bloco está na iminência de se movimentar:

Agora a segunda lei de Newton em y:

Isola a :

Agora joga esse resultado na última equação do passo 2:

Vamos isolar a F:

Vamos jogar os valores:

Agora prepara a calculadora, porque vamos calcular o valor de F para vários ângulos. O resultado está aí embaixo:

E, para o gráfico, a gente pode usar um programa de computador, ou alguma ferramenta da internet. Não tem como fazer na mão.

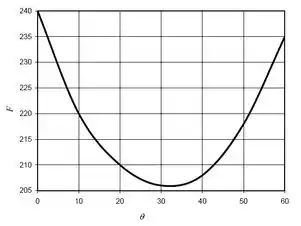
Pelo gráfico, a gente vê que a menor força ocorre para aproximadamente .